题目内容
16. 如图所示,传送带与水平地面成夹角θ=37°,以v=4m/s的速度顺时针转动,在传送带下端轻轻地放一个质量m=0.5kg的物体,它与传送带间的动摩擦因数μ=0.8,已知传送带从A到B的长度L=50m,则物体从A到B需要的时间为多少?
如图所示,传送带与水平地面成夹角θ=37°,以v=4m/s的速度顺时针转动,在传送带下端轻轻地放一个质量m=0.5kg的物体,它与传送带间的动摩擦因数μ=0.8,已知传送带从A到B的长度L=50m,则物体从A到B需要的时间为多少?
分析 物体先做匀加速直线运动,速度达到传送带速度后做匀速直线运动,根据牛顿第二定律求出开始上滑的加速度,结合速度时间公式求出速度达到传送带速度的时间,根据速度位移公式求出速度达到传送带上滑的位移,从而得出匀速运动位移,结合位移公式求出匀速运动的时间,求出总时间.
解答 解:物体放上传送带以后,受力如图,开始一段时间做匀加速运动,由牛顿第二定律得
μmgcosθ-mgsinθ=ma,
代入数据解得a=0.4m/s2
物体加速过程的时间和位移分别为${t}_{1}=\frac{v}{a}=\frac{4}{0.4}s=10s$,${s}_{1}=\frac{{v}^{2}}{2a}=\frac{16}{0.8}m=20m$<50m
由于mgsinθ<μmgcosθ,所以此后物体受到沿传送带向上的静摩擦力作用,与传送带一起匀速运动.
设物体完成剩余的位移s2所用的时间为t2,则 s2=vt2,s1+s2=L
代入数据解得 t2=7.5s
则需要的总时间t=t1+t2=17.5s
答:物体从A到B需要的时间为17.5s.
点评 解决本题的关键理清物体在传送带上的运动规律,结合牛顿第二定律和运动学公式灵活求解,难度中等.

练习册系列答案
相关题目
7.下列属于离心现象的是( )
| A. | 投篮球 | B. | 洗衣机脱水 | ||
| C. | 汽车高速转弯容易甩出车道 | D. | 旋转雨伞甩掉雨伞上的水 |
4. 如图,一小球从一半圆轨道右端c点正上方a处开始做平抛运动(小球可视为质点)飞行过程中恰好与半圆轨道相切于b点.O为半圆轨道圆,Ob与水平方向夹角为θ1,ab竖直方向的夹角为θ2.下列等式正确的是( )
如图,一小球从一半圆轨道右端c点正上方a处开始做平抛运动(小球可视为质点)飞行过程中恰好与半圆轨道相切于b点.O为半圆轨道圆,Ob与水平方向夹角为θ1,ab竖直方向的夹角为θ2.下列等式正确的是( )
 如图,一小球从一半圆轨道右端c点正上方a处开始做平抛运动(小球可视为质点)飞行过程中恰好与半圆轨道相切于b点.O为半圆轨道圆,Ob与水平方向夹角为θ1,ab竖直方向的夹角为θ2.下列等式正确的是( )
如图,一小球从一半圆轨道右端c点正上方a处开始做平抛运动(小球可视为质点)飞行过程中恰好与半圆轨道相切于b点.O为半圆轨道圆,Ob与水平方向夹角为θ1,ab竖直方向的夹角为θ2.下列等式正确的是( )| A. | tanθ1tanθ2=2 | B. | cotθ1tanθ2=2 | C. | cotθ1cotθ2=2 | D. | tanθ1cotθ2=2 |
11. 倾角为θ=37°的斜面体固定在水平地面上,一个重为100N的光滑球在水平恒力F的作用下,静止在斜面上,若将水平恒力F和斜面体对小球的支持力看成一个力,这个力的大小是( ) (g取10m/s2,sin37°=0.6,cos37°=0.8)
倾角为θ=37°的斜面体固定在水平地面上,一个重为100N的光滑球在水平恒力F的作用下,静止在斜面上,若将水平恒力F和斜面体对小球的支持力看成一个力,这个力的大小是( ) (g取10m/s2,sin37°=0.6,cos37°=0.8)
 倾角为θ=37°的斜面体固定在水平地面上,一个重为100N的光滑球在水平恒力F的作用下,静止在斜面上,若将水平恒力F和斜面体对小球的支持力看成一个力,这个力的大小是( ) (g取10m/s2,sin37°=0.6,cos37°=0.8)
倾角为θ=37°的斜面体固定在水平地面上,一个重为100N的光滑球在水平恒力F的作用下,静止在斜面上,若将水平恒力F和斜面体对小球的支持力看成一个力,这个力的大小是( ) (g取10m/s2,sin37°=0.6,cos37°=0.8)| A. | 60N | B. | 80N | C. | 100N | D. | 120N |
1.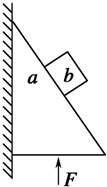 如图所示,截面为三角形的木块a上放置一铁块b,三角形木块竖直边靠在竖直且粗糙的竖直墙面上,现用竖直向上的作用力F,推动木块与铁块一起向上匀速运动,运动过程中铁块与木块始终保持相对静止,试分析物体a受到几个力( )
如图所示,截面为三角形的木块a上放置一铁块b,三角形木块竖直边靠在竖直且粗糙的竖直墙面上,现用竖直向上的作用力F,推动木块与铁块一起向上匀速运动,运动过程中铁块与木块始终保持相对静止,试分析物体a受到几个力( )
 如图所示,截面为三角形的木块a上放置一铁块b,三角形木块竖直边靠在竖直且粗糙的竖直墙面上,现用竖直向上的作用力F,推动木块与铁块一起向上匀速运动,运动过程中铁块与木块始终保持相对静止,试分析物体a受到几个力( )
如图所示,截面为三角形的木块a上放置一铁块b,三角形木块竖直边靠在竖直且粗糙的竖直墙面上,现用竖直向上的作用力F,推动木块与铁块一起向上匀速运动,运动过程中铁块与木块始终保持相对静止,试分析物体a受到几个力( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
5.从哈尔滨东站往北京的K18次列车,夕发朝至,全程运行1288km,列车运行时刻表如下:
由此可知,K18次列车全程运行时间是13.5h,列车全程的平均速度是95.4km/h.
| 哈尔滨东 | 哈尔滨 | 沈阳北 | 北京 | ||
| K18次 | 到站时间 | -- | 20:14 | 2:23 | 9:30 |
| 发车时间 | 20:00 | 20:32 | 2:31 | -- |

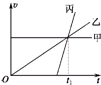 甲、乙、丙三物体从不同地点沿同一方向做直线运动,为研究他们的运动,选取该直线上的某位置为坐标原点,初速度方向为正方向,建立了位移坐标轴,现分别用速度传感器测出其在t时刻的速度大小v甲、v乙、v丙,位移传感器测出其在t时刻的位置坐标x甲、x乙、x丙,根据测出的不同时刻的速度值,得到如图所示的v-t图象,则比较t1时刻,三物体( )
甲、乙、丙三物体从不同地点沿同一方向做直线运动,为研究他们的运动,选取该直线上的某位置为坐标原点,初速度方向为正方向,建立了位移坐标轴,现分别用速度传感器测出其在t时刻的速度大小v甲、v乙、v丙,位移传感器测出其在t时刻的位置坐标x甲、x乙、x丙,根据测出的不同时刻的速度值,得到如图所示的v-t图象,则比较t1时刻,三物体( )