题目内容
8.一河道的两岸平行,河宽120m,水流速度为3m/s,一渡船相对水的速度(在静水中的速度)恒为5m/s.(1)渡船从一岸渡到另一岸所需时间至少为24s;
(2)若要渡船从一岸渡到另一岸时通过的航程最短,渡河所用时间为30s;假如水流速度变为4m/s(其它不变),若要渡船从一岸渡到另一岸时通过的航程最短,渡河所用时间变为40s.
分析 船航行时速度为静水中的速度与河水流速二者合速度,当以静水中的速度垂直河岸过河的时候渡河时间最短.由矢量合成的平行四边形定则得知小船的合速度,小船实际以合速度做匀速直线运动,进而求得位移的大小;小船以最短距离过河时,则静水中的速度斜着向上游,合速度垂直河岸.
解答 解:(1)当以静水中的速度垂直河岸过河的时候渡河时间最短,则知:tmin=$\frac{d}{{v}_{c}}$=$\frac{120}{5}$s=24s;
(2)因在静水中的速度大于水流速度,当合速度垂直河岸,小船以最短距离过河,则渡河所用时间为:
t′=$\frac{d}{\sqrt{{v}_{c}^{2}-{v}_{s}^{2}}}$=$\frac{120}{\sqrt{{5}^{2}-{3}^{2}}}$=30s;
同理,假如水流速度变为4m/s(其它不变),若要渡船从一岸渡到另一岸时通过的航程最短,渡河所用时间变为t″=$\frac{120}{\sqrt{{5}^{2}-{4}^{2}}}$=40s;
故答案为:24,30,40.
点评 小船过河问题属于运动的合成问题,要明确分运动的等时性、独立性,运用分解的思想,看过河时间只分析垂直河岸的速度,分析过河位移时,要分析合速度.

练习册系列答案
相关题目
18.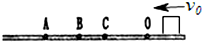 如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )
如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )
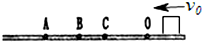 如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )
如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )| A. | $\frac{L_2}{t_2}=\frac{v_0}{2}$ | B. | $\frac{L_2}{{{t_2}^2}}>\frac{L_3}{{{t_3}^2}}$ | ||
| C. | $\frac{L_1}{t_1}<\frac{v_0}{2}$ | D. | $\frac{L_1}{{{t_1}^2}}<\frac{L_2}{{{t_2}^2}}$ |
17.下列说法正确的是( )
| A. | 物体受到恒力的冲量也可能做曲线运动 | |
| B. | 动能不变,物体的动量一定不变 | |
| C. | 动量为零时,物体一定处于平衡状态 | |
| D. | 物体所受合外力大小不变时,其动量大小一定要发生改变 |
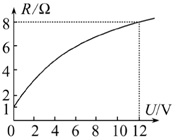 用一个额定电压为12V的灯泡做实验,测得灯丝电阻随灯泡两端电压变化关系图象如图所示.
用一个额定电压为12V的灯泡做实验,测得灯丝电阻随灯泡两端电压变化关系图象如图所示. 如图所示,传送带与水平地面成夹角θ=37°,以v=4m/s的速度顺时针转动,在传送带下端轻轻地放一个质量m=0.5kg的物体,它与传送带间的动摩擦因数μ=0.8,已知传送带从A到B的长度L=50m,则物体从A到B需要的时间为多少?
如图所示,传送带与水平地面成夹角θ=37°,以v=4m/s的速度顺时针转动,在传送带下端轻轻地放一个质量m=0.5kg的物体,它与传送带间的动摩擦因数μ=0.8,已知传送带从A到B的长度L=50m,则物体从A到B需要的时间为多少? 如图为一皮带传动装置,在传动过程中皮带不打滑,则vA=vB(填“>”“<”或“=”),ωA>ωc(填“>”“<),ωA>ωB(填“>”“<”或“=”).
如图为一皮带传动装置,在传动过程中皮带不打滑,则vA=vB(填“>”“<”或“=”),ωA>ωc(填“>”“<),ωA>ωB(填“>”“<”或“=”).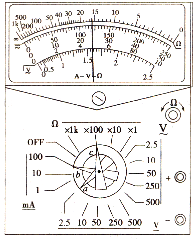 在正确操作的情况下,多用电表的指针指在图示位置.
在正确操作的情况下,多用电表的指针指在图示位置.