题目内容
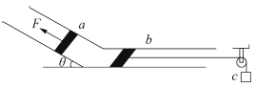
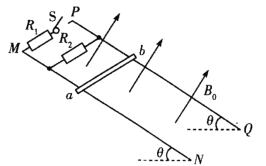
【题目】如图所示,光滑的平行金属导轨MN、PQ倾斜固定放置,导轨间距为1m,导轨所在平面的倾角为θ=30°,导轨上端并联接入阻值均为4Ω的定值电阻R1、R2,整个装置处在方向垂直导轨平面向上的匀强磁场中,磁场的磁感应强度大小为B0=2T。闭合开关S,将质量为m=1kg的金属棒ab垂直放在导轨上由静止释放。已知金属棒运动过程中始终与导轨垂直并接触良好,且导轨足够长,重力加速度g取10m/s2,不计导轨和金属棒的电阻,求:
(1)当金属棒加速度为3m/s2时,回路中的电功率为多大;
(2)某时刻,金属棒运动的速度达到最大,此时金属棒离电阻R2的距离为x0=1m,这时断开开关S,为使回路中的感应电流为零,从此时开始,匀强磁场的磁感应强度B随时间t如何变化,写出相关的表达式。
【答案】(1)2W;(2)![]()
【解析】
(1)设金属棒的加速度大小为3m/s2,回路中的电流为I。则有
![]()
解得
![]()
回路中的总电阻
![]()
回路中的电功率
P=I2R=2W
(2)设金属棒匀速运动时的速度大小为v,则有
![]()
解得
v=2.5m/s
断开开关S,当回路中的感应电流为零时有
![]()
![]()
a=gsinθ=5m/s2
代入之后解得
![]()

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目