题目内容
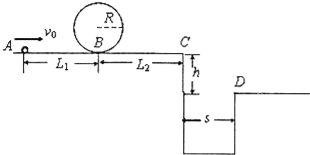
【题目】如图所示,一可看成质点的小球从A点以某一水平向右的初速度出发,沿水平直线轨道运动到B点后.进入半径R=10cm的光滑竖直圆形轨道,圆形轨间不相互重叠.即小球离开圆形轨道后可继续向C点运动,C点右侧有一壕沟,C、D两点的竖直高度h=0.8m,水平距离s=2m,水平轨道AB长为L1=5m,BC长为L2=4m,小球与水平轨道间的动摩檫因数μ=0.2.取重力加速度g=l0m/s2.则:
(1)若小球恰能通过圆形轨道的最高点,求小球在A点的初速度;
(2)若小球既能通过圆形轨道的最高点,又不掉进壕沟,求小球在A点初速度的范围是多少.
【答案】(1)5m/s(2)5m/s≤vA≤6m/s和vA≥![]() m/s
m/s
【解析】(1)小球恰能通过最高点,则有:mg=m![]()
由A到最高点的过程,由动能定理有:﹣μmgL1﹣2mgR=![]() mv2﹣
mv2﹣![]() mvA2
mvA2
解得在A点的初速度为:vA=5m/s
(2)若vA=5m/s时,设小球将停在BC间距B点x处.由动能定理得:
﹣μmg(L1+x)=0-![]() mvA2
mvA2
解得:x=1.25m
若小球刚好停在C处,则有:﹣μmg(L1+L2)=0﹣![]() mv′2A
mv′2A
解得在A点的初速度为:vA′=6m/s
若小球停在BC段,则有:5m/s≤vA≤6m/s
若小球能通过C点,并越过壕沟,则有:
h=![]() gt2
gt2
s=vct
从A到C的过程,由动能定理有:﹣μmg(L1+L2)=![]() mvC2﹣
mvC2﹣![]() mv″A2
mv″A2
则有:v″A=![]() m/s;
m/s;
故欲满足题意,初速度范围是:5m/s≤vA≤6m/s和vA≥![]() m/s(不取等号也可)
m/s(不取等号也可)

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案【题目】在“验证机械能守恒定律”实验中:
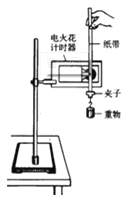
(1)运用公式![]() 对实验条件的要求是在打第一个点时,重锤恰好由静止开始下落,为此,所选择的纸带第1、2点间的距离应接近___________.
对实验条件的要求是在打第一个点时,重锤恰好由静止开始下落,为此,所选择的纸带第1、2点间的距离应接近___________.
(2)某同学实验步骤如下:
A.用天平准确测出重锤的质量; |
B.把打点计时器固定在铁架台上,并接到电源的“直流输出”上 |
C.将纸带一端固定在重锤上,另一端穿过打点计时器的限位孔,使重锤靠近打点计时器 |
D.先释放重锤,后接通电源 |
E、取下纸带,再重复几次;
F、选择纸带,测量纸带上某些点之间的距离;
G、根据测量的结果计算重锤下落过程中减少的重力势能是否等于增加的动能。
你认为他实验步骤中多余的步骤是_____________,错误的步骤是_____________(均填序号)。
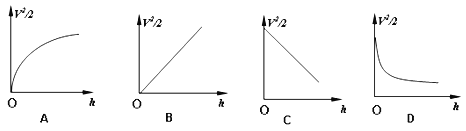
(3)在该实验中根据纸带算出相关各点的速度v,量出下落的距离h,以![]() 为纵轴,以h为横轴画出图线,则
为纵轴,以h为横轴画出图线,则![]() 图线应是图中的__________就证明机械能是守恒的,图线的斜率代表的物理量是_________.
图线应是图中的__________就证明机械能是守恒的,图线的斜率代表的物理量是_________.