题目内容
16.如图所示,甲、乙、丙三辆车(车身的长度不计)行驶在平直公路上,车速分别为6m/s,8m/s,9m/s.当甲、乙、丙三车依次相距5m时,乙车驾驶员发现甲车开始以1m/s2的加速度作匀减速运动,于是乙也立即作匀减速运动,丙车驾驶员也同样处理,最后三车均未发生撞车事故.(不考虑司机的反应时间)
问:(1)要使甲、乙两车不相撞,乙车的加速度至少应为多少?
(2)要使三车均不发生撞车事故,丙车作减速运动的加速度至少应为多少?
分析 要使乙车不追上甲车,临界情况是速度相等时两车距离为零,根据速度时间关系公式和位移时间关系公式列式求解乙车的最小加速度;同理要使丙车不追上乙车,临界情况也是速度相等时两车距离为零,根据速度时间关系公式和位移时间关系公式列式求解丙车的最小加速度.
解答 解:(1)对甲、乙分别分析,根据速度关系和位移关系有:
$\left\{\begin{array}{l}{v_1}-{a_1}t={v_2}-{a_2}t\\ 5+{v_1}t-\frac{1}{2}{a_1}{t^2}={v_2}t-\frac{1}{2}{a_2}{t^2}\end{array}\right.$
代入数据有 $\left\{\begin{array}{l}6-{a_1}t=8-{a_2}t\\ 2t-\frac{1}{2}({a_2}-1){t^2}-5=0\end{array}\right.$
解得$\left\{\begin{array}{l}t=5s\\{a_2}=\frac{7}{5}m/{s^2}\end{array}\right.$(注意在t=5s时,甲乙都还在运动)
甲停下来通过的位移 ${s_甲}=\frac{v_1^2}{{2{a_1}}}=18m$
乙停下来通过的位移${s_乙}=\frac{v_2^2}{{2{a_2}}}=\frac{8^2}{{2×\frac{7}{5}}}m=\frac{160}{7}m$
由于s甲+5>s乙,肯定不会相撞.
(2)对乙、丙分别分析,根据速度关系和位移关系有:
$\left\{\begin{array}{l}{v_2}-{a_2}t={v_3}-{a_3}t\\ 5+{v_2}t-\frac{1}{2}{a_2}{t^2}={v_3}t-\frac{1}{2}{a_3}{t^2}\end{array}\right.$
解得$t-\frac{1}{2}({a_3}-{a_2}){t^2}-5=0$,
从而得出t=10s
乙停下来花t乙=$\frac{8}{{\frac{7}{5}}}=\frac{40}{7}<10s$,乙早就停下来了,所以乙的位移为x乙=$\frac{160}{7}m$
丙的位移x丙=$\frac{v_3^2}{{2{a_3}}}≤\frac{160}{7}+5=\frac{195}{7}$,解得${a_3}≤\frac{189}{130}≈1.45m/{s^2}$.
答:(1)要使甲、乙两车不相撞,乙车的加速度至少应为$\frac{7}{5}m/{s}^{2}$;
(2)要使三车均不发生撞车事故,丙车作减速运动的加速度至少应为1.45m/s2.
点评 本题难点在于有三个小车,关键要分两次求解,明确速度相同时有最小距离,选择恰当的运动学公式很重要.

| A. | 物体零时刻的速度是2m/s | B. | 物体的加速度是4m/s2 | ||
| C. | 第3s末的速度是10m/s | D. | 第3s的位移是10m |
| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | 无法确定 |
 图中,虚线a、b、c代表电场中的三个等势面,相邻两等势面之间的电势差相等,实线为一带正电的微粒仅在电场力作用下从静止起通过该区域时的运动轨迹,走向从P到Q,则下列说法错误的是( )
图中,虚线a、b、c代表电场中的三个等势面,相邻两等势面之间的电势差相等,实线为一带正电的微粒仅在电场力作用下从静止起通过该区域时的运动轨迹,走向从P到Q,则下列说法错误的是( )| A. | P点电势较高 | B. | 带电微粒过P点时的加速度较大 | ||
| C. | 带电微粒过P点时的动能较大 | D. | 带电微粒在P点时的电势能较大 |
| A. | 因为V=$\frac{2πr}{T}$,所以线速度大小与旋转半径成正比 | |
| B. | 因为ω=$\frac{V}{r}$,所以角速度与旋转半径成反比 | |
| C. | 因为ω=2πn,所以角速度与转速成正比 | |
| D. | 因为f=$\frac{1}{T}$,所以频率高物体运动得快,频率低物体运动得慢 |
| A. | 两个匀变速直线运动的合运动一定是匀变速直线运动 | |
| B. | 两个匀速直线运动的合运动一定是匀速直线运动 | |
| C. | 一个分运动是匀变速直线运动,另一个分运动是匀速直线运动,则合运动一定是曲线运动 | |
| D. | 一个分运动是匀加速直线运动,另一个分运动是匀速直线运动,则合运动一定是直线运动 |
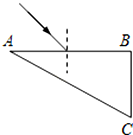 直角三角形玻璃砖ABC,其中∠A=30°,平放于水平桌面上,如图为其俯视图.一束单色光以45°的入射角水平射入其AB面,在AB面折射后又在AC面处发生一次反射,最后垂直于BC面穿出玻璃砖.
直角三角形玻璃砖ABC,其中∠A=30°,平放于水平桌面上,如图为其俯视图.一束单色光以45°的入射角水平射入其AB面,在AB面折射后又在AC面处发生一次反射,最后垂直于BC面穿出玻璃砖.