题目内容
【题目】在同一竖直线上的A、B两点，固定有等量的异种点电荷，电量为q，正、负如图所示，ΔABC为一等边三角形(边长为L)，CD与AB垂直且与右侧竖直光滑的1/4圆弧轨道的最低点C相切，已知圆弧的半径为R，现把质量为m带电量为+Q的小球(可视为质点)由圆弧的最高点M静止释放，到最低点C时速度为v0。已知静电力恒量为k，重力加速度为g，现取D为电势零点，求：
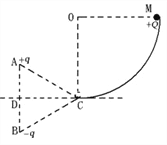
（1）小球在C点受到的电场力的大小和方向；
（2） 在最低点C轨道对小球的支持力FN多大？
（3）在等量异种电荷A、B的电场中，M点的电势φM?
【答案】（1）
（2）
（3）
【解析】试题分析：小球在C点时，受到+q和-q两个电场力作用，根据库仑定律和力的合成法求解；由牛顿运动定律，可得轨道对小球的支持力，球由最高点M运动到C的过程中，由动能定理得MC两点的电势差，又等量异种电荷中垂线上的电势相等即C、D是等电势，可得M点的电势。
（1）+Q到达最低点C时，+q与-q对其的电场力F1、F2是大小相等的，有
又因为△ABC为一等边三角形，易知F1、F2的夹角是120°
所以二者的合力为： 
，且方向是竖直向下
（2）由牛顿运动定律： 
可得轨道对小球的支持力： 
（3）小球由最高点M运动到C的过程中，由动能定理得： 
可得MC两点的电势差为： 
又等量异种电荷中垂线上的电势相等即C、D是等电势的
所以M点的电势为： 
练习册系列答案
相关题目
