题目内容
 (2011?椒江区模拟)带正电的物体A静止于绝缘水平面上,如图.现加一水平向右的匀强电场后物体开始向右运动,已知物体A与绝缘水平面间的摩擦力为电场力的一半,经一段时间后,物体的动能为Ek,此时突然使电场方向反向,大小不变,再经过一段时间后,物体回到原出发点.求:
(2011?椒江区模拟)带正电的物体A静止于绝缘水平面上,如图.现加一水平向右的匀强电场后物体开始向右运动,已知物体A与绝缘水平面间的摩擦力为电场力的一半,经一段时间后,物体的动能为Ek,此时突然使电场方向反向,大小不变,再经过一段时间后,物体回到原出发点.求:(1)物体A回到原出发点时的动能;
(2)上述前一段时间t1跟后一段时间t2的比值.
分析:(1)对加速过程、减速过程和向后的加速过程分别运用动能定理列式求解;
(2)对加速、减速、反向加速过程运用牛顿第二定律和运动学公式列式分析即可.
(2)对加速、减速、反向加速过程运用牛顿第二定律和运动学公式列式分析即可.
解答:(1)设摩擦力大小为f,电场力为F,第一阶段位移大小为x1,电场力反向后向右运动的位移大小为x2,向左运动的位移大小为x3
由题意,f=
F
第一阶段Ek=(F-f)x1=
Fgx1
电场力反向后0-Ek=-(F+f)x2
可得x2=
x1
又由题意x3=x2+x1=
x1
向左运动阶段Ek末=(F-f)x3=
F?
x1=
Ek
物体A回到原出发点时的动能为
Ek.
(2)设在后一段时间里,用t2a的时间使物体速度为零,然后用t2b的时间使物体加速回到原出发点;用a表示物体在前一段时间里的加速度,分别用a1、a2表示物体在t2a、t2b时间内的加速度,则
=
=
所以
=
=
由位移公式,得到
=
=
故
=
=
即前一段时间t1跟后一段时间t2的比值为
.
由题意,f=
| 1 |
| 2 |
第一阶段Ek=(F-f)x1=
| 1 |
| 2 |
电场力反向后0-Ek=-(F+f)x2
可得x2=
| 1 |
| 3 |
又由题意x3=x2+x1=
| 4 |
| 3 |
向左运动阶段Ek末=(F-f)x3=
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
物体A回到原出发点时的动能为
| 4 |
| 3 |
(2)设在后一段时间里,用t2a的时间使物体速度为零,然后用t2b的时间使物体加速回到原出发点;用a表示物体在前一段时间里的加速度,分别用a1、a2表示物体在t2a、t2b时间内的加速度,则
| a1 |
| a |
| F+f |
| F-f |
| 3 |
| 1 |
所以
| t2a |
| t1 |
| ||
|
| 1 |
| 3 |
由位移公式,得到
| t2b |
| t1 |
|
|
故
| t1 |
| t2 |
| t1 |
| t2a+t2b |
| 3 | ||
1+2
|
即前一段时间t1跟后一段时间t2的比值为
| 3 | ||
1+2
|
点评:本题关键是将滑块的运动过程分割成加速、减速和反向加速三段过程,然后分别运用动能定理、牛顿第二定律、运动学公式列式求解.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 (2011?椒江区模拟)如图所示,图1中一个物体连接一个轻弹簧,在水平恒力F的作用下:当水平地面光滑物体匀加速运动时,弹簧的长度为l1;当水平地面粗糙物体正好做匀速运动时,弹簧的长度为l2.图2中,弹簧测力计外壳质量为m0,所用弹簧与图1中的相同,挂钩的质量忽略不计,挂钩吊着一质量为m的重物,现用一竖直向上的与图1中相同大小的力F拉弹簧:如果向上匀加速运动,弹簧长度为l3;如果向下匀加速运动,弹簧长度为l4;下列说法正确的是( )
(2011?椒江区模拟)如图所示,图1中一个物体连接一个轻弹簧,在水平恒力F的作用下:当水平地面光滑物体匀加速运动时,弹簧的长度为l1;当水平地面粗糙物体正好做匀速运动时,弹簧的长度为l2.图2中,弹簧测力计外壳质量为m0,所用弹簧与图1中的相同,挂钩的质量忽略不计,挂钩吊着一质量为m的重物,现用一竖直向上的与图1中相同大小的力F拉弹簧:如果向上匀加速运动,弹簧长度为l3;如果向下匀加速运动,弹簧长度为l4;下列说法正确的是( )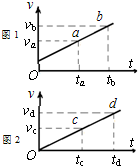 (2011?椒江区模拟)图1、图2均为质点的速度(v)--时间(t)图象,关于四边形的面积,以下说法正确的是( )
(2011?椒江区模拟)图1、图2均为质点的速度(v)--时间(t)图象,关于四边形的面积,以下说法正确的是( ) (2011?椒江区模拟)如图所示,斜面体M静止在粗糙的水平地面上,物块m恰好能在斜面体上匀速下滑.若用平行斜面的力推物块,使物块沿斜面做简谐运动而斜面保持静止,则地面对于斜面体的摩擦力Ff与时间t的关系图象应是( )
(2011?椒江区模拟)如图所示,斜面体M静止在粗糙的水平地面上,物块m恰好能在斜面体上匀速下滑.若用平行斜面的力推物块,使物块沿斜面做简谐运动而斜面保持静止,则地面对于斜面体的摩擦力Ff与时间t的关系图象应是( )