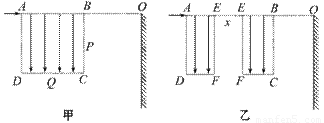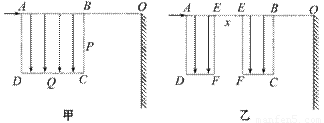题目内容
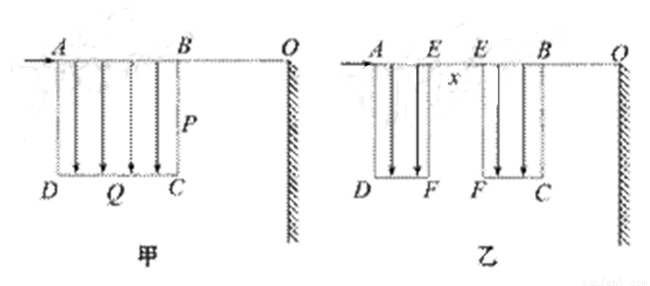
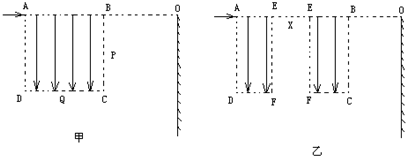
如图甲所示,边长为L的正方形区域ABCD内有竖直向下的匀强电场,电场强度为E,与区域边界BC相距L处竖直放置足够大的荧光屏,荧光屏与AB延长线交于O点.现有一质量为m,电荷量为+q的粒子从A点沿AB方向以一定的初速进入电场,恰好从BC边的中点P飞出,不计粒子重力.
(1)求粒子进入电场前的初速度的大小?
(2)其他条件不变,增大电场强度使粒子恰好能从CD边的中点Q飞出,求粒子从Q点飞出时的动能?
(3)现将电场分成AEFD和EBCF相同的两部分,并将EBCF向右平移一段距离x(x≤L),如图乙所示.设粒子打在荧光屏上位置与O点相距y,请求出y与x的关系?
(1)求粒子进入电场前的初速度的大小?
(2)其他条件不变,增大电场强度使粒子恰好能从CD边的中点Q飞出,求粒子从Q点飞出时的动能?
(3)现将电场分成AEFD和EBCF相同的两部分,并将EBCF向右平移一段距离x(x≤L),如图乙所示.设粒子打在荧光屏上位置与O点相距y,请求出y与x的关系?

分析:(1)粒子在电场中做类平抛运动,根据平抛运动的知识分别在水平方向和竖直方向上列式计算,即可得出粒子进入电场前的初速度大小.
(2)结合第一问,分析当电场变化后,粒子水平位移和竖直位移的变化情况,再分别在水平方向和竖直方向上列式,可得电场变为原来的8倍,从而可求出粒子从Q点飞出时的动能.
(3)根据题意画出粒子的轨迹图,(在电场中做类平抛运动,在电场外做匀速直线运动)通过几何知识,分析粒子两次飞出电场时速度与水平方向的夹角与相应距离的关系,便可求出y与x的关系.
(2)结合第一问,分析当电场变化后,粒子水平位移和竖直位移的变化情况,再分别在水平方向和竖直方向上列式,可得电场变为原来的8倍,从而可求出粒子从Q点飞出时的动能.
(3)根据题意画出粒子的轨迹图,(在电场中做类平抛运动,在电场外做匀速直线运动)通过几何知识,分析粒子两次飞出电场时速度与水平方向的夹角与相应距离的关系,便可求出y与x的关系.
解答:解:
(1)粒子在电场内做类平抛运动,在水平方向有:L=v0t
在竖直方向上有:
=
×
×t2
联立以上两式得:v0=
(2)其它条件不变,增大电场强度,从CD边中点Q飞出与从BC边中点P飞出相比,水平位移减半,竖直位移加倍,根据类平抛运动知识有:
水平方向:
=v0t′
竖直方向:L=
at′2
则加速度为原来8倍,电场强度为原来8倍,电场力做功为:W1=8EqL
粒子从CD边中点Q飞出时的动能:Ek1=
mv02+W1=
qEL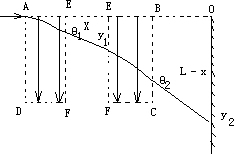
(3)将EBCF向右平移一段距离x,粒子在电场中的类平抛运动分成两部分,在无电场区域做匀速直线运动,轨迹如图所示,有一下几何关系:
tanθ1=
=
y1=xtanθ1=
tanθ2=
=1
y2=(L-x)tanθ2=L-x
y=y1+y2+
=
L-
x
答:(1)粒子进入电场前的初速度的大小为
;
(2)其他条件不变,增大电场强度使粒子恰好能从CD边的中点Q飞出,粒子从Q点飞出时的动能为
qEL;
(3)y与x的关系为y=
L-
x.
(1)粒子在电场内做类平抛运动,在水平方向有:L=v0t
在竖直方向上有:
| L |
| 2 |
| 1 |
| 2 |
| qE |
| m |
联立以上两式得:v0=
|
(2)其它条件不变,增大电场强度,从CD边中点Q飞出与从BC边中点P飞出相比,水平位移减半,竖直位移加倍,根据类平抛运动知识有:
水平方向:
| L |
| 2 |
竖直方向:L=
| 1 |
| 2 |
则加速度为原来8倍,电场强度为原来8倍,电场力做功为:W1=8EqL
粒子从CD边中点Q飞出时的动能:Ek1=
| 1 |
| 2 |
| 17 |
| 2 |

(3)将EBCF向右平移一段距离x,粒子在电场中的类平抛运动分成两部分,在无电场区域做匀速直线运动,轨迹如图所示,有一下几何关系:
tanθ1=
| ||
|
| 1 |
| 2 |
y1=xtanθ1=
| x |
| 2 |
tanθ2=
| ||
|
y2=(L-x)tanθ2=L-x
y=y1+y2+
| L |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
答:(1)粒子进入电场前的初速度的大小为
|
(2)其他条件不变,增大电场强度使粒子恰好能从CD边的中点Q飞出,粒子从Q点飞出时的动能为
| 17 |
| 2 |
(3)y与x的关系为y=
| 3 |
| 2 |
| 1 |
| 2 |
点评:该题考查了带电粒子在有界匀强电场中的偏转问题,解答此类问题,主要是利用平抛运动的知识进行求解(水平方向上是匀速直线运动,竖直方向上是匀加速直线运动);解答此类问题,有时还要用到能量的观点;对于第三问的解答,要结合粒子的运动轨迹,这就要求我们要准确的画出粒子的运动轨迹图,并应用相关的数学知识进行解答.

练习册系列答案
相关题目