题目内容
（11分）在光滑的水平面上，一质量为mA=0.1kg的小球A，以8 m/s的初速度向右运动，与质量为mB=0.2kg的静止小球B发生弹性正碰。碰后小球B滑向与水平面相切、半径为R=0.5m的竖直放置的光滑半圆形轨道，且恰好能通过最高点N后水平抛出。g=10m/s2。求：
（1） 碰撞后小球B的速度大小；
（2） 小球B从轨道最低点M运动到最高点N的过程中所受合外力的冲量；
（3） 碰撞过程中系统的机械能损失。
（1）
；（2）（
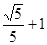）N?s，方向向左；（3）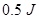
解析试题分析：（1）小球B恰好能通过圆形轨道最高点，有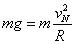
（1分）
解得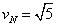
m/s 方向向左 （1分）
小球B从轨道最低点C运动到最高点D的过程中机械能守恒
有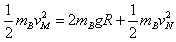
（1分）
联立①②解得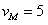
m/s （1分）
（2）设向右为正方向，合外力对小球B的冲量为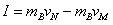
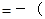
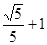
N?s，方向向左（2分）
（3）碰撞过程中动量守恒，有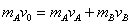
水平面光滑所以式中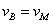
解得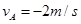
（2分）
碰撞过程中损失的机械能为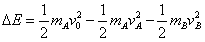
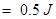（3分）
考点：机械能守恒定律，动量守恒定律，动量定理，向心力公式
练习册系列答案
相关题目
在不计空气阻力的情况下，下列运动过程满足机械能守恒的是（ ）
| A．电梯匀速下降过程 |
| B．物体从手中抛出后的运动过程 |
| C．起重机吊起重物过程 |
| D．子弹穿过木块过程 |
在下列所描述的运动过程中，若物体所受的空气阻力均可忽略不计，则机械能守恒的是 （ ）
| A．小孩沿滑梯匀速滑下 |
| B．电梯中的货物随电梯一起匀速下降 |
| C．发射过程中的火箭加速上升 |
| D．被投掷出的铅球在空中运动 |
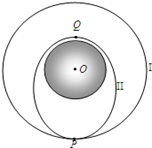
（取无穷远处引力势能为零），其中m为此时“嫦娥三号”的质量。若“嫦娥三号”在轨道II上运动的过程中，动能和引力势能相互转化，它们的总量保持不变。已知“嫦娥三号”经过Q点的速度大小为v，请根据能量守恒定律求它经过P点时的速度大小；
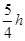）处自由下落，与斜面做无能量损失的碰撞后水平抛出．小球自由下落的落点距斜面左侧的水平距离x满足一定条件时，小球能直接落到水平地面上．
的斜面，倾角为60°，其顶端与弧形轨道末端相接，斜面正中间有一竖直放置的直杆，现让质量为1Kg的物块从弧形轨道的顶端由静止开始滑下，物块离开弧形轨道后刚好能从直杆的顶端通过，重力加速度取10m/s2，求：
）