题目内容
如图所示,长为L细线的一端固定在 A点,另一端系质量为m的小球,AB是过A的竖直线,且AB=L,E为AB的中点,过E作水平线 EF,在EF上某一位置钉一小钉D。现将小球悬线拉至水平,然后由静止释放,不计线与钉碰撞时的机械能损失。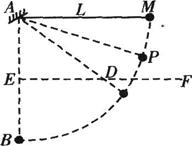
(1)若钉子在E点位置,则小球经过B点前瞬间,求绳子拉力T的大小。
(2)若小球要恰好能绕钉子在竖直平面内做圆周运动,求钉子钉在D的位置离E点的距离x。
(3)保持小钉在(2)问中的D位置不变,让小球从图示的P点静止释放,当小球运动到最低点时,若细线刚好达到最大张力而断开,且小球运动的轨迹经过B点。试求细线能承受的最大张力Tm.
(1) ;(2)
;(2) ;(3)T=
;(3)T=
解析试题分析:(1)令小球落到B点的速度为v,据机械能守恒有: ① (1分)
① (1分)
过B点前,根据牛顿运动定律 ② (1分)
② (1分)
解①②得: (1分)
(1分)
(2)小球恰好在竖直平面内做圆周运动,在最高点速度为 ,半径为R,D点距E点x,则
,半径为R,D点距E点x,则 ③(1分)
③(1分)
又  ④ (1分)
④ (1分)
由几何关系: ⑤ (1分)
⑤ (1分)
联立以上三式得:
 (2分)
(2分)
(3)小球做圆周运动在最低点的速度为v2,据牛顿运动定律有 ⑥ ( 1分)
⑥ ( 1分)
线断后小球做平抛运动轨迹过B点,
水平方向 ⑦ (1分)
⑦ (1分)
竖直方向 ⑧ (1分)
⑧ (1分)
由⑦⑧⑨可得:T= (1分)
(1分)
考点:机械能守恒定律;牛顿第二定律;向心力.

练习册系列答案
相关题目
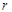 为0.2m,在圆心O处固定一个电荷量为-
为0.2m,在圆心O处固定一个电荷量为-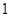 .0×
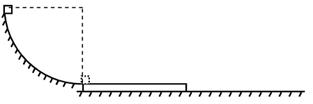
.0×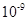 C的点电荷。质量为0.06kg、略小于圆管截面的带电小球,从与O点等高的A点沿圆管内由静止运动到最低点B ,到达B点小球刚好与圆弧没有作用力,然后从B点进入板距d= 0.08m的两平行板电容器后刚好能在水平方向上做匀速直线运动,且此时电路中的电动机刚好能正常工作。已知电源的电动势为12V,内阻为1Ω,定值电阻R的阻值为6Ω,电动机的内阻为0.5Ω.求(取g=10m/s2,静电力常量k="9.0" ×109 N·m2/C2)
C的点电荷。质量为0.06kg、略小于圆管截面的带电小球,从与O点等高的A点沿圆管内由静止运动到最低点B ,到达B点小球刚好与圆弧没有作用力,然后从B点进入板距d= 0.08m的两平行板电容器后刚好能在水平方向上做匀速直线运动,且此时电路中的电动机刚好能正常工作。已知电源的电动势为12V,内阻为1Ω,定值电阻R的阻值为6Ω,电动机的内阻为0.5Ω.求(取g=10m/s2,静电力常量k="9.0" ×109 N·m2/C2)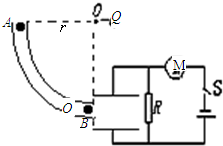

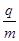 =2.0×106C/kg,粒子重力不计,计算结果保留两位有效数字。求:
=2.0×106C/kg,粒子重力不计,计算结果保留两位有效数字。求: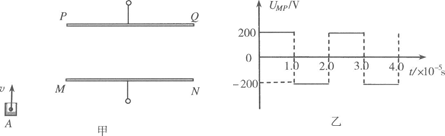
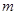 =0.8
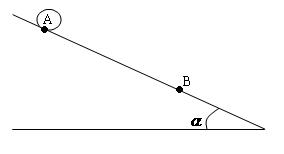
=0.8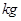 的小球A放在光滑的倾角
的小球A放在光滑的倾角 =30°绝缘斜面上,小球带正电,电荷量为
=30°绝缘斜面上,小球带正电,电荷量为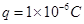 ,在斜面上的B点固定一个电荷量为
,在斜面上的B点固定一个电荷量为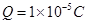 的正点电荷,将小球A由距B点0.3
的正点电荷,将小球A由距B点0.3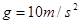 ,静电力常量
,静电力常量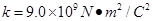 )
) 

 .
. ,且每隔T/2变向1次。现将质量为m的带正电,且电荷量为q的粒子束从AB的中点O以平行于金属板的方向OO′射入,设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T。不计重力的影响,试问:
,且每隔T/2变向1次。现将质量为m的带正电,且电荷量为q的粒子束从AB的中点O以平行于金属板的方向OO′射入,设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T。不计重力的影响,试问:
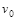 ;
;