题目内容
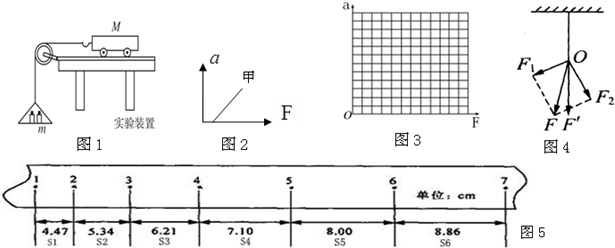
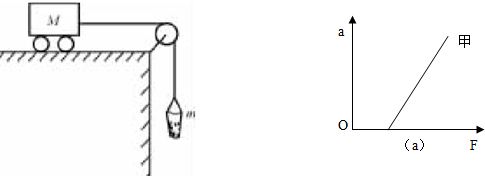
在“验证牛顿运动定律”的实验中,采用如图所示的实验装置,小车及车中的砝码的质量用M表示,小桶及沙子的质量用m表示,小车的加速度可由小车后拖动的纸带上打的点计算出.
(1)当M与m的大小关系满足
(2)一组同学在做加速度与质量的关系实验时,保持小桶及沙子的质量一定,改变小车及车中砝码的质量,测出相应的加速度,采用图象法处理数据,为了比较容易地检查出加速度a与质量M的关系,应该作a与
的图象.
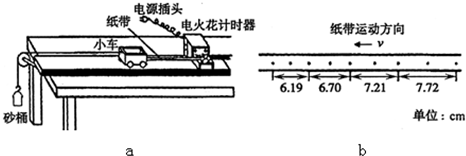
(3)如图(a)所示为甲同学根据测量数据作出的a-F图线,此图线说明实验存在的问题是
(1)当M与m的大小关系满足
M>>m
M>>m
时,才可以认为绳对小车的拉力等于盘及盘中砝码的重力.(2)一组同学在做加速度与质量的关系实验时,保持小桶及沙子的质量一定,改变小车及车中砝码的质量,测出相应的加速度,采用图象法处理数据,为了比较容易地检查出加速度a与质量M的关系,应该作a与
| 1 |
| M |
| 1 |
| M |
(3)如图(a)所示为甲同学根据测量数据作出的a-F图线,此图线说明实验存在的问题是
没有(完全)平衡小车受到的摩擦力
没有(完全)平衡小车受到的摩擦力
.
分析:(1)要求在什么情况下才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力,需求出绳子的拉力,而要求绳子的拉力,应先以整体为研究对象求出整体的加速度,再以M为研究对象求出绳子的拉力,通过比较绳对小车的拉力大小和盘和盘中砝码的重力的大小关系得出只有m<<M时才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力.
(2)反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系;正比例函数图象是过坐标原点的一条直线,就比较容易判定自变量和因变量之间的关系.
(3)图中有拉力时没有加速度,说明没有(完全)平衡小车受到的摩擦力.
(2)反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系;正比例函数图象是过坐标原点的一条直线,就比较容易判定自变量和因变量之间的关系.
(3)图中有拉力时没有加速度,说明没有(完全)平衡小车受到的摩擦力.
解答:解:(1)以整体为研究对象有mg=(m+M)a
解得a=
以M为研究对象有绳子的拉力F=Ma=
mg
显然要有F=mg必有m+M=M,故有M>>m,即只有M>>m时才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力.
(2)根据牛顿第二定律F=Ma,a与M成反比,而反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系,故不能作a-M图象;但a=
,
故a与
成正比,而正比例函数图象是过坐标原点的一条直线,就比较容易判定自变量和因变量之间的关系,故应作a-
图象;
(3)图中有拉力时没有加速度,说明没有(完全)平衡小车受到的摩擦力.
故答案为:(1)M>>m (2)
(3)没有(完全)平衡小车受到的摩擦力
解得a=
| mg |
| m+M |
以M为研究对象有绳子的拉力F=Ma=
| M |
| m+M |
显然要有F=mg必有m+M=M,故有M>>m,即只有M>>m时才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力.
(2)根据牛顿第二定律F=Ma,a与M成反比,而反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系,故不能作a-M图象;但a=
| F |
| M |
故a与
| 1 |
| M |
| 1 |
| M |
(3)图中有拉力时没有加速度,说明没有(完全)平衡小车受到的摩擦力.
故答案为:(1)M>>m (2)
| 1 |
| M |
(3)没有(完全)平衡小车受到的摩擦力
点评:只要真正掌握了实验原理就能顺利解决此类实验题目,而实验步骤,实验数据的处理都与实验原理有关,故要加强对实验原理的学习和掌握.

练习册系列答案
相关题目
某同学在“验证牛顿运动定律”的实验中,保持小车所受的合力F的大小不变,改变小车的质量m,得到了不同m时的加速度大小a,并绘出了a-
的图象,则( )
| 1 |
| m |
| A、图象是一条直线,直线的斜率表示小车受到的合力的倒数 |
| B、图象是一条直线,直线的斜率表示小车受到的合力 |
| C、图象是一条曲线,曲线各点的切线斜率表示小车受到的合力的倒数 |
| D、图象是一条曲线,曲线各点的切线斜率表示小车受到的合力 |