��Ŀ����
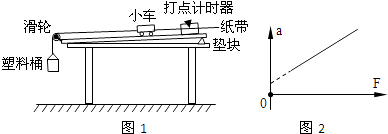
����Ŀ��ijͬѧ����ͼ1��ʾ��װ�ã�����������С��ͬ��С����������ײ����֤�����غ㶨�ɣ�ͼ��AB��б�ۣ�BC��ˮƽ�ۣ���������ƽ����O��Ϊ��ˮƽ��ĩ��C���ش�����ָ��λ�ã�ʵ��ʱ�Ȳ����ñ�����2������1��б���ϵ�ijһ�̶�λ��G�ɾ�ֹ��ʼ���£��䵽λ��ˮƽ����ļ�¼ֽ�ϣ����ºۼ����ظ�10�Σ��õ���1����ƽ��λ��ΪP��Ȼ����2����ˮƽ��ĩ�ˣ�����1�Դ�λ��G�ɾ�ֹ���£�����2��ײ����������ֱ��ڼ�¼ֽ�����¸��Եĺۼ����ظ�10�Σ�ʵ��õ���С�������ƽ��λ�÷ֱ�ΪM��N��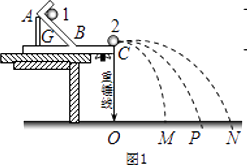
��1���ڸ�ʵ���У�����Ҫ�õ����������������е� �� ����ѡ�⡢����ţ�
A.��ƽ
B.�̶ȳ�
C.���
D.��С��ͬ�ĸ����Ӳ�����һ��
��2���ڴ�ʵ���У���1������Ϊm1 �� ��2������Ϊm2 �� ������m1m2��ѡ����ڡ�����С�ڡ����ڡ�����
��3��������2���е�ˮƽ������ͼ���߶α�ʾ��
��4��ij��ʵ���еó�����������ͼ2��ʾ��������ײ�����ж����غ㣬������С������m1�ͱ���С������m2֮��Ϊ �� 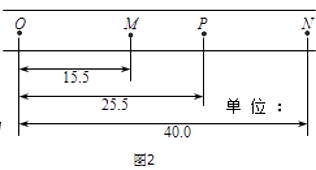
��5��������ײ�ǵ�����ײ�����߶�OM��ON��OPӦ����Ĺ�ϵ�ǣ���ֻ���߶�OM��ON��OP��ʾ����
���𰸡�
��1��C
��2������
��3��ON
��4��4��1
��5��OP=OM+ON
���������⣺��1��Ϊ�����ʵ�飬Ӧ��Ҫ������С��ȣ��������ȵ���С����ҪD��
����С����ײ������ˮƽ�������غ㶨�ɣ����У�
m1v0=m1v1+m2v2
����ƽ���˶��Ĺ���������ʱ������ȵģ����Եã�
tm1v0=tm1v1+tm2v2
����m1OP=m1OM+m2ON
��֪����Ҫʹ����ƽ����С���������ʹ�ÿ̶ȳ߲���С����ˮƽ�����λ�ƣ�����ҪAB����ʵ���в���Ҫ�������ѡC��
��2����С����ײ������ˮƽ�������غ㶨�ɹ��У�m1v0=m1v1+m2v2
����ײ�����ж����غ���У� ![]() m1v02=
m1v02= ![]() m1v12+
m1v12+ ![]() m2v22
m2v22
��ã�v1= ![]() v0
v0
Ҫ��������С����ٶ�v1��0����m1��m2��0��
���Դ��ǣ����ڣ���3��1���2����ײ��2����ٶ�����1����ٶȼ�С������ƽ���˶�����ֱ�߶���ͬ������������ײ��2�����ص���N�㣬���Ա�����2���е�ˮƽ������ͼ���߶�ON��ʾ����4����ͼ�����ݿ�֪��OM=15.5cm��OP=25.5cm��ON=40.0cm��
����붯���غ����ʽ��֪��m1��m2=4��1����5��������С������Ϊm1������С������Ϊm2����ײǰ�������ٶ�Ϊv0����ײ�������ٶȷֱ�Ϊv1��v2��
���ݶ����غ�úͻ�е�غ㶨�ɵã�
m1v0=m1v1+m2v2
![]() m1v02=
m1v02= ![]() m1v12+
m1v12+ ![]() m2v22
m2v22
������ã�
v0+v1=v2
����ƽ���˶�ʱ����ͬ����õ���
OP+OM=ON��
�ʣ�OP=ON��OM
���Դ��ǣ���1��C����2�����ڣ���3��ON����4��4��1����5��OP=OM+ON