题目内容
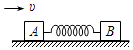
【题目】如图所示,甲、乙两车的质量均为M,静置在光滑的水平面上,两车相距为L,乙车上站立着一个质量也为M的人,他通过一条水平轻绳用恒定的水平拉力F拉甲车直到两车相碰,在此过程中( )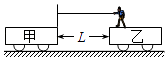
A.甲、乙两车运动过程中某时刻瞬时速度之比为1:2
B.甲、乙两车运动的距离之比为2:1
C.人拉绳所做的功为FL
D.人拉绳所做的功为 ![]() FL
FL
【答案】B,C
【解析】解:A、甲、乙和两车组成的系统合外力为零,系统的动量守恒,取向右为正方向,由动量守恒定律得:
0=Mv甲﹣(M+M)v乙;
可得甲、乙两车运动中速度之比为:v甲:v乙=(M+M):M=2:1,A符合题意;
B、设甲车和乙车移动的距离分别为s1和s2.则有:v甲= ![]() ,v乙=
,v乙= ![]()
又 s1+s2=L
联立解得:s1:s2=2:1,s1= ![]() L,s2=
L,s2= ![]() L,B符合题意;
L,B符合题意;
CD、根据功的定义可知,此过程中人拉绳所做功等于拉力和人相对于绳子的位移的乘积,为W=FL.C符合题意,D不符合题意
故答案为:BC
整个系统为研究对像 满足动量守恒根据动量守恒和做功的条件综合求解。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目