题目内容
【题目】如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场中.一质量为m、带电荷量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小为E(E小于![]() ).
).
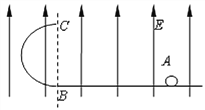
(1)试计算物块在运动过程中克服摩擦力做的功;
(2)证明物块离开轨道落回水平面过程的水平距离与场强大小E无关,且为一常量;
【答案】(1)![]() (2) S=2R
(2) S=2R
【解析】试题分析:(1)物块恰能通过圆弧最高点C时,圆弧轨道与物块间无弹力作用,物块受到的重力和电场力提供向心力,再对物块在由A运动到C的过程中,运用动能定理列式即可求解;物块离开半圆形轨道后做类平抛运动,设水平位移为s,根据平抛运动的特点即可求解.
(1)物块恰能通过圆弧最高点C时,圆弧轨道与物块间无弹力作用,物块受到的重力和电场力提供向心力![]() ①
①
物块在由A运动到C的过程中,设物块克服摩擦力做的功为![]() ,根据动能定理有
,根据动能定理有![]() ②
②
由①②式解得![]() ③
③
(2)物块离开半圆形轨道后做类平抛运动,设水平位移为s,则
水平方向有![]() ④,竖直方向有
④,竖直方向有![]() ⑤
⑤
由①④⑤式联立解得![]() ⑥
⑥
因此,物块离开轨道落回水平面的水平距离与场强大小E无关,大小为2R.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目