题目内容
11. 质量m=3kg的质点静止在光滑水平面上的直角坐标系的原点O(坐标系所在平面即为水平面),先用沿+x轴方向的力F1=9N作用了2s,然后撤去F1;再用沿+y轴方向的力F2=24N作用了1s,请列出必要的表达式,计算出质点在3s末的位置坐标并在图中画出质点在这3s内的质点的运动轨迹.
质量m=3kg的质点静止在光滑水平面上的直角坐标系的原点O(坐标系所在平面即为水平面),先用沿+x轴方向的力F1=9N作用了2s,然后撤去F1;再用沿+y轴方向的力F2=24N作用了1s,请列出必要的表达式,计算出质点在3s末的位置坐标并在图中画出质点在这3s内的质点的运动轨迹.
分析 前2s,物体在F1作用下在x轴方向做匀加速直线运动;撤去F1,施加F2,由于合力与速度方向垂直,做曲线运动,将曲线运动分解为x轴方向和y轴方向研究,在x轴方向做匀速直线运动,在y轴方向做匀加速直线运动.
解答  解:前2s,根据牛顿第二定律,有:
解:前2s,根据牛顿第二定律,有:
a1=$\frac{{F}_{1}}{m}=\frac{9}{3}=3m/{s}^{2}$
速度为:
v1=a1t1=3×2=6m/s
位移:
x1=$\frac{1}{2}a{t}_{1}^{2}$=$\frac{1}{2}×3×{2}^{2}$=6m
第3s,物体做类似平抛运动,加速度:
a2=$\frac{{F}_{2}}{m}=\frac{24}{3}=8m/{s}^{2}$
水平分位移:
x2=v1t2=6×1=6m
y方向分位移:
$y=\frac{1}{2}{a}_{2}{t}_{2}^{2}=\frac{1}{2}×8×{1}^{2}=4m$
3s末横坐标:x=6+6=12m;
故3s末的坐标为:(12m,4m)
答:质点在3s末的坐标为:(12m,4m).
点评 本题关键明确各个时间段物体的受力情况和运动情况,然后结合类平抛运动的分运动公式列式求解,不难.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 2011年8月,“嫦娥二号”成功进入了绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家.如图所示,该拉格朗日点位于太阳与地球连线的延长线上,一飞行器位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,则此飞行器的( )
2011年8月,“嫦娥二号”成功进入了绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家.如图所示,该拉格朗日点位于太阳与地球连线的延长线上,一飞行器位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,则此飞行器的( )
 2011年8月,“嫦娥二号”成功进入了绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家.如图所示,该拉格朗日点位于太阳与地球连线的延长线上,一飞行器位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,则此飞行器的( )
2011年8月,“嫦娥二号”成功进入了绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家.如图所示,该拉格朗日点位于太阳与地球连线的延长线上,一飞行器位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,则此飞行器的( )| A. | 向心力仅由地球的引力提供 | B. | 向心力仅由太阳的引力提供 | ||
| C. | 线速度大于地球的线速度 | D. | 向心加速度大于地球的向心加速度 |
2. 如图所示是负点电荷周围的一条电场线,电场线上A、B两点的电场强度分别为EA、EB,电势分别为φA、φB,下列判断中正确的是( )
如图所示是负点电荷周围的一条电场线,电场线上A、B两点的电场强度分别为EA、EB,电势分别为φA、φB,下列判断中正确的是( )
 如图所示是负点电荷周围的一条电场线,电场线上A、B两点的电场强度分别为EA、EB,电势分别为φA、φB,下列判断中正确的是( )
如图所示是负点电荷周围的一条电场线,电场线上A、B两点的电场强度分别为EA、EB,电势分别为φA、φB,下列判断中正确的是( )| A. | EA>EB,φA>φB | B. | EA<EB,φA>φB | C. | EA>EB,φA<φB | D. | EA=EB,φA=φB |
19.把行星围绕太阳的运动近似看作匀速圆周运动,开普勒第三定律可写为$\frac{{r}^{3}}{{T}^{2}}$=k,其中r为轨道半径,T为公转周期.若m为行星质量,G为万有引力常量,则可推知( )
| A. | 行星受太阳的引力为k$\frac{m}{{r}^{2}}$ | B. | 行星受太阳的引力为k$\frac{2{π}^{2}m}{{r}^{2}}$ | ||
| C. | 太阳的质量为$\frac{4{π}^{2}k}{G}$ | D. | 太阳的密度为$\frac{3πk}{G{r}^{3}}$ |
6. 如图所示,一根质量不计的轻杆绕水平固定转轴O在竖直平面内做顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到的图中位置时,轻直对小球作用力的方向可能为( )
如图所示,一根质量不计的轻杆绕水平固定转轴O在竖直平面内做顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到的图中位置时,轻直对小球作用力的方向可能为( )
 如图所示,一根质量不计的轻杆绕水平固定转轴O在竖直平面内做顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到的图中位置时,轻直对小球作用力的方向可能为( )
如图所示,一根质量不计的轻杆绕水平固定转轴O在竖直平面内做顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到的图中位置时,轻直对小球作用力的方向可能为( )| A. | 沿F2的方向 | B. | 沿F3的方向 | C. | 沿F1的方向 | D. | 沿F4的方向 |
16. 如图所示,某人用同一水平力F先后两次从静止开始拉同一物体,第一次使此物体沿光滑水平面前进L的距离,第二次使此物体沿粗糙水平面也前进L的距离.若先后两次拉力做的功分别为W1和W2,平均功率分别为P1和P2,则( )
如图所示,某人用同一水平力F先后两次从静止开始拉同一物体,第一次使此物体沿光滑水平面前进L的距离,第二次使此物体沿粗糙水平面也前进L的距离.若先后两次拉力做的功分别为W1和W2,平均功率分别为P1和P2,则( )
 如图所示,某人用同一水平力F先后两次从静止开始拉同一物体,第一次使此物体沿光滑水平面前进L的距离,第二次使此物体沿粗糙水平面也前进L的距离.若先后两次拉力做的功分别为W1和W2,平均功率分别为P1和P2,则( )
如图所示,某人用同一水平力F先后两次从静止开始拉同一物体,第一次使此物体沿光滑水平面前进L的距离,第二次使此物体沿粗糙水平面也前进L的距离.若先后两次拉力做的功分别为W1和W2,平均功率分别为P1和P2,则( )| A. | W1=W2,P1=P2 | B. | W1=W2,P1>P2 | C. | W1>W2,P1>P2 | D. | W1>W2,P1=P2 |
20. 滑雪运动员沿斜坡从A下滑到B的过程中,重力对他做功为2000J,他克服阻力做功为100J,则他的重力势能( )
滑雪运动员沿斜坡从A下滑到B的过程中,重力对他做功为2000J,他克服阻力做功为100J,则他的重力势能( )
 滑雪运动员沿斜坡从A下滑到B的过程中,重力对他做功为2000J,他克服阻力做功为100J,则他的重力势能( )
滑雪运动员沿斜坡从A下滑到B的过程中,重力对他做功为2000J,他克服阻力做功为100J,则他的重力势能( )| A. | 减小了2000J | B. | 减小了100J | C. | 增加了2000J | D. | 减小了1900J |
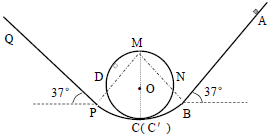 如图所示,ABCDMNC′PQ为竖直轨道.其中,CDMNC′是圆心为O、半径为R=0.1m的圆轨道.BC和C′P都是半径为2R的圆弧轨道,圆心为M点.MOC(C′)在同一竖直线上.直轨道AB和PQ分别相切与圆弧轨道的B、P两点,直轨道与水平方向的夹角均为37°.PQ是动摩擦因数为μ=0.5的粗糙轨道,其余轨道均光滑.现将质量m=0.2kg的小滑块(可视为质点)从距离B点L=4m的A处静止释放.求:(已知sin37°=0.6,cos37°=0.8,g取10m/s2)
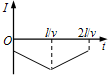
如图所示,ABCDMNC′PQ为竖直轨道.其中,CDMNC′是圆心为O、半径为R=0.1m的圆轨道.BC和C′P都是半径为2R的圆弧轨道,圆心为M点.MOC(C′)在同一竖直线上.直轨道AB和PQ分别相切与圆弧轨道的B、P两点,直轨道与水平方向的夹角均为37°.PQ是动摩擦因数为μ=0.5的粗糙轨道,其余轨道均光滑.现将质量m=0.2kg的小滑块(可视为质点)从距离B点L=4m的A处静止释放.求:(已知sin37°=0.6,cos37°=0.8,g取10m/s2) 如图,两相距为l的平行虚线之间存在垂直纸面向里的匀强磁场.abcd是位于纸面内的直角梯形线圈,ab与dc间的距离也为l.t=0时刻,ab边与磁场区域边界重合(如图).现令线圈以恒定的速度v沿垂直于磁场区域边界的方向穿过磁场区域.取沿a→d→c→b→a的感应电流为正,则在线圈穿越磁场区域的过程中,感应电流I随时间t变化的图线可能是( )
如图,两相距为l的平行虚线之间存在垂直纸面向里的匀强磁场.abcd是位于纸面内的直角梯形线圈,ab与dc间的距离也为l.t=0时刻,ab边与磁场区域边界重合(如图).现令线圈以恒定的速度v沿垂直于磁场区域边界的方向穿过磁场区域.取沿a→d→c→b→a的感应电流为正,则在线圈穿越磁场区域的过程中,感应电流I随时间t变化的图线可能是( )