题目内容
19.把行星围绕太阳的运动近似看作匀速圆周运动,开普勒第三定律可写为$\frac{{r}^{3}}{{T}^{2}}$=k,其中r为轨道半径,T为公转周期.若m为行星质量,G为万有引力常量,则可推知( )| A. | 行星受太阳的引力为k$\frac{m}{{r}^{2}}$ | B. | 行星受太阳的引力为k$\frac{2{π}^{2}m}{{r}^{2}}$ | ||
| C. | 太阳的质量为$\frac{4{π}^{2}k}{G}$ | D. | 太阳的密度为$\frac{3πk}{G{r}^{3}}$ |
分析 根据引力提供向心力,结合向心力的公式,以及开普勒第三定律求出天涯对行星的引力大小.根据万有引力公式可求得质量.
解答 解:A、行星绕太阳运动,靠引力提供向心力,则有:F=mr$\frac{4{π}^{2}}{{T}^{2}}$…①
根据开普勒第三定律知:T2=$\frac{{r}^{3}}{k}$…②
将②代入①得:F=$4{π}^{2}k\frac{m}{{r}^{2}}$,故A、B错误;
C、由$\frac{GMm}{{r}^{2}}$=$4{π}^{2}k\frac{m}{{r}^{2}}$可得:M=$\frac{4{π}^{2}k}{G}$;故C正确.
D、由于不明确太阳的半径,故无法求得太阳的密度;故D错误;
故选:C.
点评 解决本题的关键知道行星绕太阳做圆周运动向心力的来源,掌握向心力公式、开普勒第三定律,并能灵活运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
10. 如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:(取g=10m/s2)
如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:(取g=10m/s2)
(1)人与雪橇从A到B的过程中,损失的机械能为多少?
(2)设人与雪橇在BC段所受阻力恒定,求阻力的大小.
(3)人与雪橇从B到C的过程中,运动的距离.
 如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:(取g=10m/s2)
如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:(取g=10m/s2) | 位置 | A | B | C |
| 速度(m/s) | 2.0 | 12.0 | 0 |
| 时刻(s) | 0 | 4 | 10 |
(2)设人与雪橇在BC段所受阻力恒定,求阻力的大小.
(3)人与雪橇从B到C的过程中,运动的距离.
7.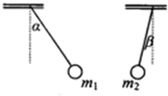 如图所示,两个小球的质量分别为m1和m2,带电量分别为q1和q2,用长度不等的轻丝线悬挂起来,两丝线与竖直方向的夹角分别为α和β(α>β),两小球在同一水平线上,那么( )
如图所示,两个小球的质量分别为m1和m2,带电量分别为q1和q2,用长度不等的轻丝线悬挂起来,两丝线与竖直方向的夹角分别为α和β(α>β),两小球在同一水平线上,那么( )
 如图所示,两个小球的质量分别为m1和m2,带电量分别为q1和q2,用长度不等的轻丝线悬挂起来,两丝线与竖直方向的夹角分别为α和β(α>β),两小球在同一水平线上,那么( )
如图所示,两个小球的质量分别为m1和m2,带电量分别为q1和q2,用长度不等的轻丝线悬挂起来,两丝线与竖直方向的夹角分别为α和β(α>β),两小球在同一水平线上,那么( )| A. | q1一定大于q2 | |
| B. | m1一定小于m2 | |
| C. | $\frac{{q}_{1}}{{m}_{1}}$一定等于$\frac{{q}_{2}}{{m}_{2}}$ | |
| D. | m1所受库仑力一定大于m2所受的库仑力 |
14.下列说法正确的是( )
| A. | 若物体的运动状态发生改变,则它一定做曲线运动 | |
| B. | 若物体做曲线运动,则它的运动状态一定改变 | |
| C. | 竖直平面内做匀速圆周运动的物体,其合外力可能不指向圆心 | |
| D. | 匀速直线运动和初速度为零的匀加速直线运动的合运动一定是曲线运动 |
 一列简谐横波在x轴上传播,在t1=0时刻波形如图中实线所示,t2=0.2s时刻波形如图中虚线所示,求:
一列简谐横波在x轴上传播,在t1=0时刻波形如图中实线所示,t2=0.2s时刻波形如图中虚线所示,求: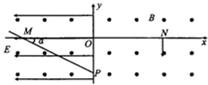 在垂直纸面向外、磁感应强度为B=1T的匀强磁场中,建立如图所示的竖直直角坐标系xOy,在x<0的区域内有沿x轴负向的匀强电场,场强大小为E=$\sqrt{3}$V/m,在x>0的区域也存在匀强电场(图中未画出).一个带正电油滴从x轴上的N点竖直向下做匀速圆周运动至P点后进入x<0的区域,沿着与水平方向成α=30°角斜向上做直线运动,通过x轴上的M点,已知重力加速度为g=10m/s2,求:
在垂直纸面向外、磁感应强度为B=1T的匀强磁场中,建立如图所示的竖直直角坐标系xOy,在x<0的区域内有沿x轴负向的匀强电场,场强大小为E=$\sqrt{3}$V/m,在x>0的区域也存在匀强电场(图中未画出).一个带正电油滴从x轴上的N点竖直向下做匀速圆周运动至P点后进入x<0的区域,沿着与水平方向成α=30°角斜向上做直线运动,通过x轴上的M点,已知重力加速度为g=10m/s2,求: 质量m=3kg的质点静止在光滑水平面上的直角坐标系的原点O(坐标系所在平面即为水平面),先用沿+x轴方向的力F1=9N作用了2s,然后撤去F1;再用沿+y轴方向的力F2=24N作用了1s,请列出必要的表达式,计算出质点在3s末的位置坐标并在图中画出质点在这3s内的质点的运动轨迹.
质量m=3kg的质点静止在光滑水平面上的直角坐标系的原点O(坐标系所在平面即为水平面),先用沿+x轴方向的力F1=9N作用了2s,然后撤去F1;再用沿+y轴方向的力F2=24N作用了1s,请列出必要的表达式,计算出质点在3s末的位置坐标并在图中画出质点在这3s内的质点的运动轨迹. 某实验小组采用如图1所示的装置探究功与速度变化的关系,小车在橡皮筋的作用下弹出后,沿木板滑行.打点计时器的工作频率为50Hz.
某实验小组采用如图1所示的装置探究功与速度变化的关系,小车在橡皮筋的作用下弹出后,沿木板滑行.打点计时器的工作频率为50Hz.