题目内容
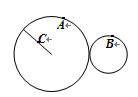
如图所示,O1为皮带传动装置的主动轮的轴心,轮的半径为r1;O2为从动轮的轴心,轮的半径为r2;r3为与从动轮固定在一起的大轮的半径.已知r2=1.5r1,r3 =2r1.A、B、C分别是三个轮边缘上的点,那么质点A、B、C的线速度之比是_________,角速度之比是_________ ,向心加速度之比是__________.

3∶3∶4. 3∶2∶2 9∶6∶8
分析:对于A与B,由于皮带不打滑,线速度大小相等.对于B与C绕同一转轴转动,角速度相等,由v=ωr研究A与B的角速度关系,以及B与C的线速度关系.
解答:解:对于A与B,由于皮带不打滑,线速度大小相等,即vA=vB.由v=ωr得ωA:ωB=r2:r1=3:2.
对于B与C,绕同一转轴转动,角速度相等,即ωB=ωC.由v=ωr得vB:vC=r3:r2=3:4.
则vA:vB:vC=3:3:4,ωA:ωB:ωC=3:2:2
根据向心加速度 ,因为AB线速度相等,所以aA:aB=r2:r1=3:2=9:6,因为BC角速度相等,所以aB:aC=r2:r3=3:4=6:8,所以aA:aB:aC=9:6:8
,因为AB线速度相等,所以aA:aB=r2:r1=3:2=9:6,因为BC角速度相等,所以aB:aC=r2:r3=3:4=6:8,所以aA:aB:aC=9:6:8
故答案为:3:3:4,3:2:2,9:6:8.
点评:本题运用比例法解决物理问题的能力,关键抓住相等的量:对于不打滑皮带传动的两个轮子边缘上各点的线速度大小相等;同一轮上各点的角速度相同.
解答:解:对于A与B,由于皮带不打滑,线速度大小相等,即vA=vB.由v=ωr得ωA:ωB=r2:r1=3:2.
对于B与C,绕同一转轴转动,角速度相等,即ωB=ωC.由v=ωr得vB:vC=r3:r2=3:4.
则vA:vB:vC=3:3:4,ωA:ωB:ωC=3:2:2
根据向心加速度
 ,因为AB线速度相等,所以aA:aB=r2:r1=3:2=9:6,因为BC角速度相等,所以aB:aC=r2:r3=3:4=6:8,所以aA:aB:aC=9:6:8
,因为AB线速度相等,所以aA:aB=r2:r1=3:2=9:6,因为BC角速度相等,所以aB:aC=r2:r3=3:4=6:8,所以aA:aB:aC=9:6:8故答案为:3:3:4,3:2:2,9:6:8.
点评:本题运用比例法解决物理问题的能力,关键抓住相等的量:对于不打滑皮带传动的两个轮子边缘上各点的线速度大小相等;同一轮上各点的角速度相同.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

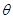 的粗糙直轨道,BECD是圆心为O的光滑圆轨道,半径为R,与AB在B点相切. 一质量为m质点,从直轨道上P点由静止释放,P、O、C三点在同一水平直线上,E为最低点,质点与AB直轨道动摩擦因数为
的粗糙直轨道,BECD是圆心为O的光滑圆轨道,半径为R,与AB在B点相切. 一质量为m质点,从直轨道上P点由静止释放,P、O、C三点在同一水平直线上,E为最低点,质点与AB直轨道动摩擦因数为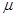 ,重力加速度为g,求:
,重力加速度为g,求: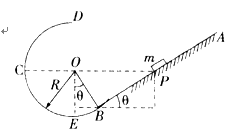
 点,则
点,则
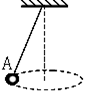
 的细线把一个小球吊在天花板上的
的细线把一个小球吊在天花板上的 点,在
点,在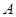 点,然后由静止释放,如图所示,小球落到
点,然后由静止释放,如图所示,小球落到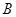 点后,恰好能够绕着
点后,恰好能够绕着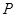 点完成竖直平面内的圆周运动,求:
点完成竖直平面内的圆周运动,求: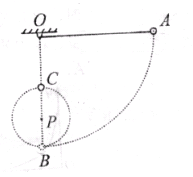
 竖直放置的光滑细圆管,O为细圆管的圆心,BO与竖直线的夹角为45°;在圆管的末端C连接一光滑水平面,水平面上一质量为M=1.5kg的木块与一轻质弹簧拴接,轻弹簧的另一端固定于竖直墙壁上。现有一质量为m=0.5kg的小球从O点正上方某处A点以v0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始即受到始终竖直向上的恒力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失。小球过后与木块发生完全非弹性碰撞(g=10m/s2)。求:
竖直放置的光滑细圆管,O为细圆管的圆心,BO与竖直线的夹角为45°;在圆管的末端C连接一光滑水平面,水平面上一质量为M=1.5kg的木块与一轻质弹簧拴接,轻弹簧的另一端固定于竖直墙壁上。现有一质量为m=0.5kg的小球从O点正上方某处A点以v0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始即受到始终竖直向上的恒力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失。小球过后与木块发生完全非弹性碰撞(g=10m/s2)。求: