题目内容
【题目】已知地球半径为R,月球半径为r,地球与月球之间的距离(两球中心之间的距离)为L。月球绕地球公转的周期为T1,地球自转的周期为T2,地球绕太阳公转周期为T3,假设公转运动都视为圆周运动,万有引力常量为G,由以上条件可知( )
A.地球的质量为![]() B.月球的质量为
B.月球的质量为![]()
C.地球的密度为![]() D.月球绕地球运动的加速度为
D.月球绕地球运动的加速度为![]()
【答案】CD
【解析】
A. 月球围绕地球圆周运动,已知月球公转的周期为T1,公转半径为L,根据万有引力提供向心力
![]()
可得地球质量![]() ,故A错误;
,故A错误;
B. 因为月球是环绕天体,万有引力提供向心力等式两边消去环绕天体的质量,故无法求得月球的质量,故B错误;
C. 地球的密度为
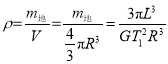
故C正确;
D. 月球绕地球公转,万有引力提供圆周运动向心力有
![]()
月球绕地球运动的加速度为![]() ,故D正确。
,故D正确。
故选CD。

练习册系列答案
相关题目