题目内容
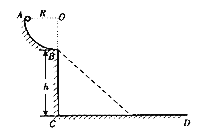
【题目】如图所示,轨道 ABCD 的 AB 段为一半径 R =0.2 m 的光滑![]() 圆形轨道BC段为高为 h =5 m 的竖直轨道,CD 段为水平轨道。一质量为 0.1 kg 的小球由 A 点从静止开始下滑到 B 点时速度的大小为 2 m /s,离开 B 点做平抛运动(g 取 10 m /s2),求:
圆形轨道BC段为高为 h =5 m 的竖直轨道,CD 段为水平轨道。一质量为 0.1 kg 的小球由 A 点从静止开始下滑到 B 点时速度的大小为 2 m /s,离开 B 点做平抛运动(g 取 10 m /s2),求:
(1)小球离开 B 点后,在 CD 轨道上的落地点到 C 的水平距离;
(2)小球到达 B 点时对圆形轨道的压力大小?
(3)如果在 BCD轨道上放置一个倾角=45°的斜面(如图中虚线所示),那么小球离开 B 点后能否落到斜面上?如果能,求它第一次落在斜面上时下落的高度。
【答案】(1)2m(2)3N(3)能,0.8m
【解析】
解:(1)设小球离开![]() 点做平抛运动的时间为
点做平抛运动的时间为![]() ,落地点到
,落地点到![]() 点距离为
点距离为![]()
竖直方向:![]()
解得:![]()
水平方向:![]()
(2)小球达![]() 受重力
受重力![]() 和向上的弹力
和向上的弹力![]() 作用,根据向心力公式和牛顿第二定律得:
作用,根据向心力公式和牛顿第二定律得:![]()
解得:![]()
由牛顿第三定律知球对![]() 的压力
的压力![]() ,即小球到达
,即小球到达![]() 点时对圆形轨道的压力大小为3N,方向竖直向下
点时对圆形轨道的压力大小为3N,方向竖直向下
(3)如图,斜面的倾角![]() ,则有
,则有![]()
因为![]() ,所以小球离开
,所以小球离开![]() 点后能落在斜面上,
点后能落在斜面上,
假设小球第一次落在斜面上![]() 点,
点,![]() 长为
长为![]() ,小球从
,小球从![]() 点到
点到![]() 点的时间为
点的时间为![]()
则有:![]() ,
,![]()
联立解得:![]()
它第一次落在斜面上时下落的高度:![]()

练习册系列答案
相关题目