题目内容
【题目】如图所示,两块相同平板P1P2置于光滑水平面上,质量均为m;P2的右端固定一轻质弹簧,左端A与弹簧的自由端B相距L.物体P置于P1的最右端,质量为2m且可看作质点.P1与P以共同速度v0向右运动,与静止的P2发生碰撞,碰撞时间极短.碰撞后P1与P2粘连在一起.P压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内).P与P2之间的动摩擦因数为μ.求:
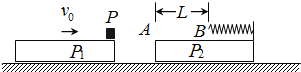
(1)P1、P2刚碰完时的共同速度v1和P的最终速度v2;
(2)此过程中弹簧的最大压缩量x和相应的弹性势能Ep
【答案】(1)![]() v0;
v0;![]() v0(2)
v0(2)![]() ;
;![]() mv02
mv02
【解析】
试题分析:(1)P1、P2碰撞过程,由动量守恒定律
mv0=2mv1 ①
解得v1=![]() v0 ,方向水平向右 ②
v0 ,方向水平向右 ②
对P1、P2、P系统,由动量守恒定律
mv0+2mv0=4mv2③
解得v2=![]() v0 ,方向水平向右④
v0 ,方向水平向右④
(2)当弹簧压缩最大时,P1、P2、P三者具有共同速度v2,由动量守恒定律
mv0+2mv0=4mv2 ⑤
对系统由能量守恒定律
μ(2m)g×2(L+x)=![]() (2m)v02+
(2m)v02+![]() (2m)v12-
(2m)v12-![]() (4m)v22⑥
(4m)v22⑥
解得![]() ⑦
⑦
最大弹性势能Ep=![]() (m+m)v02+
(m+m)v02+![]() (2m)v12-
(2m)v12-![]() (m+m+2m)v22-μ2mg(L+x) ⑧
(m+m+2m)v22-μ2mg(L+x) ⑧
解得Ep=![]() mv02⑨
mv02⑨

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目