题目内容
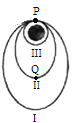
【题目】嫦娥系列卫星靠近月球时被月球引力捕获,经过椭圆轨道Ⅰ和Ⅱ的调整 ,最终进入近月圆轨道Ⅲ,并开展对月球的探测,P为三个轨道的相交点,下列说法正确的是( )
A. 嫦娥系列卫星的发射速度必须大于第二宇宙速度
B. 卫星在轨道Ⅱ的远月点Q的速度可能大于圆轨道Ⅲ的线速度
C. 卫星在三个轨道经过P点时加速度都相同
D. 卫星在轨道Ⅰ上机械能最大
【答案】CD
【解析】
根据线速度与轨道半径的关系,比较卫星在Q做圆周运动的速度与圆轨道Ⅲ的线速度大小关系,结合变轨的原理比较卫星在轨道Ⅱ的远月点Q的速度与圆轨道Ⅲ的线速度.根据万有引力大小关系,结合牛顿第二定律比较加速度.根据线速度的大小关系,抓住势能相等,比较在不同轨道P点的机械能,从而确定哪个轨道机械能最大。
A项:卫星的发射速度大于第二宇宙速度,将脱离地球的束缚,绕太阳运动,故A错误;
B项:根据![]() 知,若Q点做匀速圆周运动的速度小于圆轨道Ⅲ的线速度,从Q点进入圆轨道需加速,可知Q点的速度一定小于圆轨道Ⅲ的线速度,故B错误;
知,若Q点做匀速圆周运动的速度小于圆轨道Ⅲ的线速度,从Q点进入圆轨道需加速,可知Q点的速度一定小于圆轨道Ⅲ的线速度,故B错误;
C项:卫星在三个轨道上的P点所受的万有引力相等,根据牛顿第二定律知,加速度相同,故C正确;
D项:根据椭圆轨道半长轴的大小知,卫星在轨道I上P点的速度最大,轨道Ⅲ上P点的速度最小,由于势能相等,则卫星在轨道I上的机械能最大,故D正确。
故应选CD。

练习册系列答案
相关题目