题目内容
【题目】如图a所示，水平直线MN下方有竖直向上的匀强电场，现将一重力不计，比荷 
=1×106C/kg的正电荷置于电场中的O点由静止释放，经过 
×10﹣5s后，电荷以v0=1.5×104m/s的速度通过MN进入其上方的匀强磁场，磁场与纸面垂直，磁感应强度B按图b所示规律周期性变化（图b中磁场方向以垂直纸面向外为正方向，以电荷第一次通过MN时为t=0时刻）．计算结果可用π表示，求：
（1）O点与直线MN之间的电势差；
（2）t= 
×10﹣5s时刻电荷与O点的水平距离
（3）如果在O点右方d=67.5cm处有一垂直于MN的足够大的挡板，求电荷从O点出发运动到挡板所需要的时间．
【答案】
（1）解：电荷在电场中做匀加速直线运动，由动能定理得：
，
解得： 
V．
答：O点与直线MN之间的电势差为1.125×102V；
（2）当磁场垂直纸面向外时，设电荷运动的半径为r1，
则 
，
解得： 
，
周期为： 
．
当磁场垂直纸面向里时，电荷运动的半径为： 
=0.03m=3cm．
周期为： 
．
电荷从t=0时刻开始做周期性运动，其运动轨迹如图甲所示，t= 
时刻电荷与O点的水平距离为：
△d=2（r1﹣r2）=4cm．
答：t= 
×10﹣5s时刻电荷与O点的水平距离为4cm．
（3）电荷从第一次通过MN开始，其运动的周期T= 
，
根据电荷的运动情况可知，电荷到达挡板前运动的完整周期数为15个，此时电荷沿MN运动的距离：15△d=60cm．
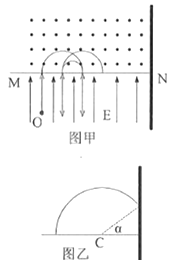
则最后7.5cm的运动轨迹如乙图所示，有：r1+r1cosα=7.5cm．
解得cosα=0.5，则α=60°，
故电荷运动的总时间为： 
s．
答：电荷从O点出发运动到挡板所需要的时间为 
．
【解析】本题主要考查带电粒子在电场中，磁场中的运动问题。电荷在电场中运动，牛顿第二定律结合运动学公式是常见的解题方法，电荷在磁场中运动时，因为其具有周期性，根据轨迹求解时间。
【考点精析】解答此题的关键在于理解带电微粒（计重力）在电场中的运动的相关知识，掌握带电颗粒:如液滴、油滴、尘埃、小球等，除有说明或明确的暗示以外，一般都不能忽略重力；由于带电粒子在匀强电场中所受电场力与重力都是恒力，因此可以用两种方法处理:①正交分解法;②等效“重力”法．
