题目内容
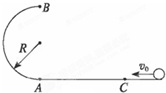 如图所示,半径R的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.10kg的小球,以初速度v0=7.0m/s在水平地面上向左做加速度a=3.0m/s2的匀减速直线运动,运动4.0m后,冲上竖直半圆环,恰能通过最高点B而不脱离轨道,最后小球落在C点,(g=10m/s2),求
如图所示,半径R的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.10kg的小球,以初速度v0=7.0m/s在水平地面上向左做加速度a=3.0m/s2的匀减速直线运动,运动4.0m后,冲上竖直半圆环,恰能通过最高点B而不脱离轨道,最后小球落在C点,(g=10m/s2),求(1)小球到达A点的速度.
(2)轨道半径R.
(3)A、C间的距离.
分析:(1)对从C到A过程运用速度位移公式列式求解;
(2)小球冲上竖直半圆环,恰能通过最高点B而不脱离轨道,重力恰好提供向心力;再结合机械能守恒定律列式;然后联立方程组求解;
(3)从C到B做平抛运动,根据平抛运动的分位移公式列式求解.
(2)小球冲上竖直半圆环,恰能通过最高点B而不脱离轨道,重力恰好提供向心力;再结合机械能守恒定律列式;然后联立方程组求解;
(3)从C到B做平抛运动,根据平抛运动的分位移公式列式求解.
解答:解:(1)从C到A过程做匀加速直线运动,根据速度位移公式,有
-
=2(-a)x
解得
vA=
=
=5m/s
(2)A到B过程,机械能守恒,有
mg?2R=
m
-
m
①
球恰好经过B点,在B点,重力恰好提供向心力,有
mg=m
②
联立解得
R=
=
=0.5m
vB=
m/s
(3)小球从C到B做平抛运动,根据平抛运动的分位移公式,有
水平方向:x=vBt
竖直方向:2R=
gt2
解得
x=1m
答:(1)小球到达A点的速度为5m/s;
(2)轨道半径R0.5m;
(3)A、C间的距离为1m.
| v | 2 A |
| v | 2 0 |
解得
vA=
|
| 49-2×3×4 |
(2)A到B过程,机械能守恒,有
mg?2R=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
球恰好经过B点,在B点,重力恰好提供向心力,有
mg=m
| ||
| R |
联立解得
R=
| ||
| 5g |
| 25 |
| 5×10 |
vB=
| 5 |
(3)小球从C到B做平抛运动,根据平抛运动的分位移公式,有
水平方向:x=vBt
竖直方向:2R=
| 1 |
| 2 |
解得
x=1m
答:(1)小球到达A点的速度为5m/s;
(2)轨道半径R0.5m;
(3)A、C间的距离为1m.
点评:本题综合运用了运动学公式、机械能守恒定律、牛顿第二定律、平抛运动规律,综合性较强,关键理清过程,选择适当的定理或定律进行解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一束平行光在垂直于玻璃圆柱体轴线的平面内,以θ=45°角射到半圆柱体的平面上,已知玻璃折射率n=
如图所示,一束平行光在垂直于玻璃圆柱体轴线的平面内,以θ=45°角射到半圆柱体的平面上,已知玻璃折射率n= (1)P、Q是一列简谐横波中的质点,相距30m,各自的振动图象如图所示.
(1)P、Q是一列简谐横波中的质点,相距30m,各自的振动图象如图所示.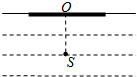 如图所示,某种液体的液面下h处有一点光源S,若将一半径为R不透明的薄片置于液面,其圆心O在S的正上方,恰好从液面上任一位置都不能看到点光源S.真空中光速用c表示.求光在液体中的传播速率v.
如图所示,某种液体的液面下h处有一点光源S,若将一半径为R不透明的薄片置于液面,其圆心O在S的正上方,恰好从液面上任一位置都不能看到点光源S.真空中光速用c表示.求光在液体中的传播速率v.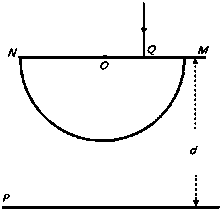 如图所示,一玻璃砖的横截面为半圆形,MN为截面的直径,Q是MN上的一点且与M点的距离QM=
如图所示,一玻璃砖的横截面为半圆形,MN为截面的直径,Q是MN上的一点且与M点的距离QM=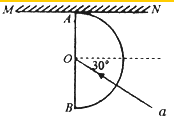 (2013?宝鸡三模)如图所示,半圆形玻璃砖的半径R=10cm,折射率n=
(2013?宝鸡三模)如图所示,半圆形玻璃砖的半径R=10cm,折射率n=