题目内容
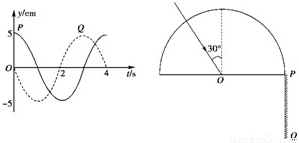
 (1)P、Q是一列简谐横波中的质点,相距30m,各自的振动图象如图所示.
(1)P、Q是一列简谐横波中的质点,相距30m,各自的振动图象如图所示.①此列波的频率f=
0.25
0.25
Hz.②如果P比Q离波源近,且P与Q间距离小于1个波长,那么波长λ=
40
40
m.③如果P比Q离波源远,那么波长λ=
| 120 |
| 4n+1 |
| 120 |
| 4n+1 |
(2)如图所示,半圆形玻璃砖的半径为R,光屏PQ置于直径的右端并与直径垂直,一复色光与竖直方向成α=30°角射入玻璃砖的圆心,由于色光中含有两种单色光,故在光屏上出现了两个光斑,玻璃对两种单色光的折射率分别为n1=
| 2 |
| 3 |
①这两个光斑之间的距离;
②为使光屏上的光斑消失,复色光的入射角至少为多少.
分析:(1)①从振动图象中读出波的周期,频率等于周期的倒数.
②如果P比Q离波源近,且P与Q间距离小于1个波长,P点在波峰位置时,Q点在平衡位置向下振动,两点之间相隔
λ,根据两点的距离得出波长的大小.
③如果P比Q离波源远,考虑波传播的周期性,两点间的距离x=(n+
)λ,n=0,1,2,3…从而求出波长的大小.
(2)①根据折射定律求出两色光从玻璃砖进入空气的折射角,再根据几何关系求出两个光斑之间的距离.
②当两种色光在界面处均发生全反射时光屏上的光斑消失,根据sinC=
求出临界角的大小.
②如果P比Q离波源近,且P与Q间距离小于1个波长,P点在波峰位置时,Q点在平衡位置向下振动,两点之间相隔
| 3 |
| 4 |
③如果P比Q离波源远,考虑波传播的周期性,两点间的距离x=(n+
| 1 |
| 4 |
(2)①根据折射定律求出两色光从玻璃砖进入空气的折射角,再根据几何关系求出两个光斑之间的距离.
②当两种色光在界面处均发生全反射时光屏上的光斑消失,根据sinC=
| 1 |
| n |
解答: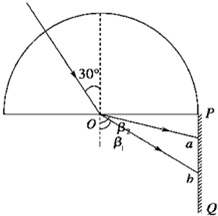 解:(1)①质点的振动周期为4s,则波的频率:
解:(1)①质点的振动周期为4s,则波的频率:
f=
=0.25Hz.
②如果P比Q离波源近,且P与Q间距离小于1个波长,有:
=30m
得:λ=40m.
③如果P比Q离波源远,有x=(n+
)λ,n=0,1,2,3…,
解得:λ=
m(n=0,1,2,3…)
故答案为:(1)0.25 (2)40 (3)
m(n=0,1,2,3…)
(2)①作出光路如图所示,由折射定律有:
n1=
,n2=
代入数据得:
=
=
解得:β1=45° β2=60°
故:ab=Pb-Pa=Rtan45°-Rtan30°=(1-
)R
②当两种色光在界面处均发生全反射时光屏上的光斑消失,折射率越小,临界角越大,当折射率为n2的色光发生全反射时,玻璃对其折射率为n1的色光先一定全反射,故sinC=
=
,即入射角α=C=45°.
答:①两个光斑之间的距离为(1-
)R.
②为使光屏上的光斑消失,复色光的入射角至少为45°.
 解:(1)①质点的振动周期为4s,则波的频率:
解:(1)①质点的振动周期为4s,则波的频率:f=
| 1 |
| T |
②如果P比Q离波源近,且P与Q间距离小于1个波长,有:
| 3λ |
| 4 |
得:λ=40m.
③如果P比Q离波源远,有x=(n+
| 1 |
| 4 |
解得:λ=
| 120 |
| 4n+1 |
故答案为:(1)0.25 (2)40 (3)
| 120 |
| 4n+1 |
(2)①作出光路如图所示,由折射定律有:
n1=
| sinβ1 |
| sinα |
| sinβ2 |
| sinα |
代入数据得:
| 2 |
| sinβ1 |
| sin30° |
| 3 |
| sinβ2 |
| sin30° |
解得:β1=45° β2=60°
故:ab=Pb-Pa=Rtan45°-Rtan30°=(1-
| ||
| 3 |
②当两种色光在界面处均发生全反射时光屏上的光斑消失,折射率越小,临界角越大,当折射率为n2的色光发生全反射时,玻璃对其折射率为n1的色光先一定全反射,故sinC=
| 1 |
| n1 |
| 1 | ||
|
答:①两个光斑之间的距离为(1-
| ||
| 3 |
②为使光屏上的光斑消失,复色光的入射角至少为45°.
点评:解决本题的关键掌握质点的振动和波动的关系,以及掌握光的折射定律和发生全反射的条件.

练习册系列答案
相关题目
 [物理--选修3-4]
[物理--选修3-4]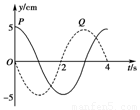
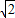 和n2=
和n2=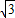 ,求:
,求: