题目内容
 (2013?宝鸡三模)如图所示,半圆形玻璃砖的半径R=10cm,折射率n=
(2013?宝鸡三模)如图所示,半圆形玻璃砖的半径R=10cm,折射率n=| 3 |
分析:光线在AB面上发生反射和折射,在水平屏幕MN上出现两个光斑,根据折射定律结合几何关系求出两个光斑之间的距离.
解答:解:画出如图光路图,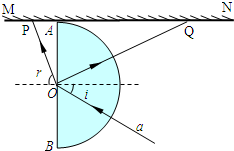 设折射角为r,根据折射定律:
设折射角为r,根据折射定律:
n=
则得:sinr=nsini=
×sin30°=
解得:r=60°
根据几何关系,两个光斑之间的距离为:
L=PA+AQ=Rtan30°+2Rsin60°=10×
+2×10×
cm=
cm
故选:C
 设折射角为r,根据折射定律:
设折射角为r,根据折射定律:n=
| sinr |
| sini |
则得:sinr=nsini=
| 3 |
| ||
| 2 |
解得:r=60°
根据几何关系,两个光斑之间的距离为:
L=PA+AQ=Rtan30°+2Rsin60°=10×
| ||
| 3 |
| ||
| 2 |
40
| ||
| 3 |
故选:C
点评:对于几何光学,作出光路图是解答的关键的依据,要注意运用结合几何知识研究两个光斑间的距离.

练习册系列答案
相关题目
 (2013?宝鸡三模)粗细均匀的U形管竖直放置,右端封闭,左管内有一个重力和摩擦都不计的活塞,管内水银把气体分隔成A、B两部分.当大气压强为P0=75cmHg、温度为t0=27℃时,管内水银面在同一高度,两部分气体的长度均为L0=20cm.
(2013?宝鸡三模)粗细均匀的U形管竖直放置,右端封闭,左管内有一个重力和摩擦都不计的活塞,管内水银把气体分隔成A、B两部分.当大气压强为P0=75cmHg、温度为t0=27℃时,管内水银面在同一高度,两部分气体的长度均为L0=20cm. (2013?宝鸡三模)(此题属多选)如图所示是某电场中的一条电场线,M、N是该电场线上的两点,则以下判断中正确的是( )
(2013?宝鸡三模)(此题属多选)如图所示是某电场中的一条电场线,M、N是该电场线上的两点,则以下判断中正确的是( ) (2013?宝鸡三模)(此题属多选)如图所示,质量为m的物体与转台之问的动摩擦因数为μ,物体与转轴间距离为R,物体随转台由静止开始转动,当转台转速增加到某一值后转台开始匀速转动,整个过程中物体相对于转台静止不动,则以下判断正确的是( )
(2013?宝鸡三模)(此题属多选)如图所示,质量为m的物体与转台之问的动摩擦因数为μ,物体与转轴间距离为R,物体随转台由静止开始转动,当转台转速增加到某一值后转台开始匀速转动,整个过程中物体相对于转台静止不动,则以下判断正确的是( ) (2013?宝鸡三模)如图所示,人用轻绳通过定滑轮吊起重物A.当人匀速向右运动的过程中,下列说法正确的是( )
(2013?宝鸡三模)如图所示,人用轻绳通过定滑轮吊起重物A.当人匀速向右运动的过程中,下列说法正确的是( )