题目内容
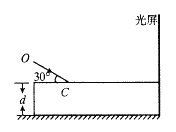
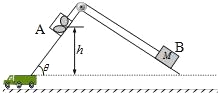
【题目】如图所示为仓储公司常采用的“自动化”货物装卸装置,两个相互垂直的斜面固定在地面上,货箱A(含货物)和配重B通过与斜面平行的轻绳跨过光滑滑轮相连.A装载货物后从h=8.0m高处由静止释放,运动到底端时,A和B同时被锁定,卸货后解除锁定,A在B的牵引下被拉回原高度处,再次被锁定.已知θ=53°,B的质量M为1.0×103kg,A、B与斜面间的动摩擦因数均为μ=0.5,滑动摩擦力与最大静摩擦力相等,g取10m/s2,sin53°=0.8,cos53°=0.6.
(1)为使A由静止释放后能沿斜面下滑,其质量m需要满足什么条件?
(2)若A的质量m=4.0×103kg,求它到达底端时的速度v;
(3)为了保证能被安全锁定,A到达底端的速率不能大于12m/s.请通过计算判断:当A的质量m不断增加时,该装置能否被安全锁定.
【答案】(1)![]() (2)
(2)![]() (3)该装置能被安全锁定.
(3)该装置能被安全锁定.
【解析】试题分析:(1)设左斜面倾角为θ,左斜面倾角为β,货箱由静止释放后能沿斜面下滑,则
F合>0 1分
mgsinθ Mgsinβ μmgcosθ μMgcosβ >0 2分
m >2.0×103kg 1分
(2)对系统应用动能定理:
由动能定理:W合=△Ek2分
mgh Mg(hsinβ/sinθ) ( μmg cosθ+μMgcosβ)(h/sinθ) ="(1/2)(M+m)" v23分
v![]() 1分
1分
另解:本小题也可用牛顿第二定律求解:
由F合=ma 1分
mgsinθ Mgsinβ μmgcosθ μMgcosβ=(M+m)a 2分
a=2m/s21分
由运动学方程 v2=2aL 1分
L=h/sinθ
v![]() 1分
1分
(3)当A的质量m与B的质量M 之间关系满足m>>M时,货箱下滑的加速度最大,
到达斜面底端的速度也最大,此时有mgsinθ μmgcosθ=mam2分
am=5m/s21分
v2=2amL 1分
货箱到达斜面底端的最大速度v=10m/s<12m/s 1分
所以,当A的质量m不断增加时,该运输装置均能被安全锁定 1分

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案