题目内容
【题目】研究光的干涉特性时,常将一束光分成两束频率相同的相干光。用如图所示装置来将光“一分为二、一块矩形玻璃砖,下底面镀银,厚为d,右端紧靠竖直光屏,一束单色光沿OC方向射到玻璃砖上表面,分成两束频率相同的相干光,一束反射后直接射到屏上A点,一束折射后经下底面反射后再经上表面折射后射到屏上B点。已知OC与玻璃砖上表面成30°角,玻璃砖对该单色光的折射率为![]() ,光在真空中的传播速度为c。图中A、B两点未画出。求:
,光在真空中的传播速度为c。图中A、B两点未画出。求:
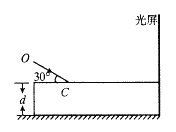
(i)射到B点的折射光在玻璃砖中传播的时间;
(ii)A、B两点之间的距离。
【答案】(i) ![]() (ii)
(ii) ![]()
【解析】①设折射光线在上表面的入射角为i1,折射角为r1,在玻璃砖中传播速度为v,传播距离为x.传播时间为t,i1=60°,则
![]()
![]()
![]()
![]()
解得:r1=30°。![]()
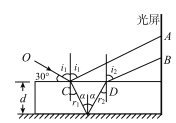
②设折射光线在下底面反射后在上表面的D点折射.C、D间距离为LCD.在下底面入射角和反射角为,在D点入射角为i2,折射角为r2.C点距光屏的距离为L.A点距玻璃砖上表面的高度为h1,B点距玻璃砖上表面的高度为h2,A、B两点间距离为h,则
![]()
![]()
h=h1-h2,=r1,r2=
![]()
LCD=2dtan
解得:=30°,i2=60°,h=![]()
点睛:本题是几何光学问题,除掌握光的折射定律的表达式以及光速与折射率的关系外,关键是作出规范的光路图,结合折射定律和几何关系进行求解.

练习册系列答案
相关题目