题目内容
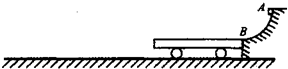
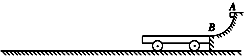 如图所示,AB为半径R=0.8m的1/4光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06m,车上表面距地面的高度h=0.2m.现有一质量m=1kg的滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求:
如图所示,AB为半径R=0.8m的1/4光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06m,车上表面距地面的高度h=0.2m.现有一质量m=1kg的滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求:(1)滑块到达B端时,轨道对它支持力的大小;
(2)车被锁定时,车右端距轨道B端的距离;
(3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小;
(4)滑块落地点离车左端的水平距离.
分析:(1)由机械能守恒定律求出滑块到B端的速度,由牛顿第二定律求出支持力.
(2)根据牛顿第二定律分别求出滑块和小车的加速度,由运动式求出两者速度相同经过的时间,确定两者的运动情况.再求解车右端距轨道B端的距离.
(3)求出滑块相对于小车的位移△x,由内能E=μmg△x求出内能.
(4)滑块滑出小车后做平抛运动,求出滑块滑到A端的速度和平抛的时间,求解滑块落地点离车左端的水平距离.
(2)根据牛顿第二定律分别求出滑块和小车的加速度,由运动式求出两者速度相同经过的时间,确定两者的运动情况.再求解车右端距轨道B端的距离.
(3)求出滑块相对于小车的位移△x,由内能E=μmg△x求出内能.
(4)滑块滑出小车后做平抛运动,求出滑块滑到A端的速度和平抛的时间,求解滑块落地点离车左端的水平距离.
解答:解:(1)设滑块到达B端时速度为v,
由机械能守恒定律,得mgR=
mv2
由牛顿第二定律,得FN-mg=m
联立两式,代入数值解得:FN=3mg=30N.
(2)当滑块滑上小车后,由牛顿第二定律,得
对滑块有:-μmg=ma1
对小车有:μmg=Ma2
设经时间t两者达到共同速度,则有:v+a1t=a2t
解得t=1 s.
由于1 s<1.5 s,此时小车还未被锁定,两者的共同速度:v′=a2t=1 m/s 两者一起匀速运动,直到小车被锁定.
故车被锁定时,车右端距轨道B端的距离:x=
a2t2+v′t′=1 m.
(3)从车开始运动到被锁定的过程中,滑块相对小车滑动的距离
△x=
t-
a2t2=2 m
故产生的内能:E=μmg△x=6 J.
(4)对滑块由动能定理,得-μmg(L-△x)=
mv″2-
mv′2
滑块脱离小车后,在竖直方向有:h=
gt″2
故滑块落地点离车左端的水平距离:x′=v″t″=0.16 m.
答:(1)滑块到达B端时,轨道对它支持力的大小为30N.
(2)车被锁定时,车右端距轨道B端的距离为1m.
(3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小为6J.
(4)滑块落地点离车左端的水平距离为0.16m.
由机械能守恒定律,得mgR=
| 1 |
| 2 |
由牛顿第二定律,得FN-mg=m
| v2 |
| R |
联立两式,代入数值解得:FN=3mg=30N.
(2)当滑块滑上小车后,由牛顿第二定律,得
对滑块有:-μmg=ma1
对小车有:μmg=Ma2
设经时间t两者达到共同速度,则有:v+a1t=a2t
解得t=1 s.
由于1 s<1.5 s,此时小车还未被锁定,两者的共同速度:v′=a2t=1 m/s 两者一起匀速运动,直到小车被锁定.
故车被锁定时,车右端距轨道B端的距离:x=
| 1 |
| 2 |
(3)从车开始运动到被锁定的过程中,滑块相对小车滑动的距离
△x=
| v+v′ |
| 2 |
| 1 |
| 2 |
故产生的内能:E=μmg△x=6 J.
(4)对滑块由动能定理,得-μmg(L-△x)=
| 1 |
| 2 |
| 1 |
| 2 |
滑块脱离小车后,在竖直方向有:h=
| 1 |
| 2 |
故滑块落地点离车左端的水平距离:x′=v″t″=0.16 m.
答:(1)滑块到达B端时,轨道对它支持力的大小为30N.
(2)车被锁定时,车右端距轨道B端的距离为1m.
(3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小为6J.
(4)滑块落地点离车左端的水平距离为0.16m.
点评:本题之处在于分析滑块和小车速度相同所经历的时间,与1.5s进行比较来分析两者的运动情况.求摩擦生热Q=f△x,△x是相对位移.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图所示,AB为半径R=0.8m的1/4光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06m,车上表面距地面的高度h=0.2m.现有一质量m=1kg的滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求:
如图所示,AB为半径R=0.8m的1/4光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06m,车上表面距地面的高度h=0.2m.现有一质量m=1kg的滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求: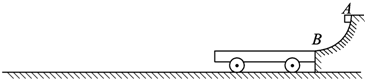
 如图所示,AB为半径R=2m的一段光滑圆糟,A、B两点在同一水平高度上,且AB弧长10cm.将一小球从A点由静止开始释放,则它第一次运动到B点所用时间为( )
如图所示,AB为半径R=2m的一段光滑圆糟,A、B两点在同一水平高度上,且AB弧长10cm.将一小球从A点由静止开始释放,则它第一次运动到B点所用时间为( )