题目内容
【题目】根据光的粒子性，光的能量是不连续的，而是一份一份的，每一份叫一个光子，光子具有动量和能量。已知光在真空中的速度为c，普朗克常量为h。
（1）请根据爱因斯坦质能方程和光子说证明光子动量的表达式为P=
，并由此表达式可以说明光具有什么特性？
（2）实验表明：光子与速度不太大的电子碰撞发生散射时，光的波长会变长或者不变，这种现象叫康普顿散射，该过程遵循能量守恒定律和动量守恒定律。如果电子具有足够大的初速度，以至于在散射过程中有能量从电子转移到光子，则该散射被称为逆康普顿散射，这一现象已被实验证实。关于上述逆康普顿散射，请定性分析散射光的波长将如何变化？
（3）惯性质量和引力质量是两个不同的物理概念。万有引力定律公式中的质量称为引力质量，它表示物体产生引力场或变引力作用的本领，一般用天平称得的物体质量就是物体的引力质量。牛顿第二定律公式中的质量称为惯性质量，它是物体惯性的量度，用惯性秤可以确定物体的惯性质量。频率为
的一个光子具有惯性质量，此质量由相对论知识可以推得可由光子的能量确定，请通过本题陈述和所给已知量确定光子的惯性质量m的表达式。
（4）接第三问，假定光子也有引力质量，量值等于惯性质量。据相对论等近代物理知识可知：从一颗星球表面发射出的光子，逃离星球引力场时，该光子的引力质量会随着光子的运动而发生变化，光子的能量将不断地减少。
a.试分析该光子的波长将如何变化？
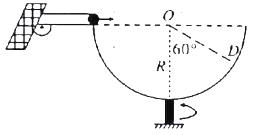
b.若给定万有引力常量G，星球半径R，光子的初始频率，光子从这颗星球（假定该星球为质量分布均匀的圆球体）表面到达无穷远处的频移（频率变化量值）为
，假定<<,星球和光子系统的引力势能表达式为：
（选定光子和星球相距无穷远处为零势能处），此表达式中的r为光子到星球中心的距离，试求该星球的质量M。
【答案】(1) 波粒二象性；（2）散射光的波长将会变小；（3）
；（4）a．波长将会变大；b. 
；
【解析】(1)根据爱因斯坦质能方程和光子说可以得到光子能量E=
；
光子动量P=mc=
，光子动量表达式：P=h/λ，说明光具有波粒二象性。
(2)因为在散射过程中有能量从电子转移到光子，则光子的能量增大，因为光子的能量
E=
，故散射光的波长将会变小。
(3)根据本题陈述和所给已知量确定光子的惯性质量m的表达式为
(4)a．因为光子能量减小，根据E=可知，该光子的波长将会变大。
b.根据能量守恒定律可知：光子能量的损失量等于星球与光子系统的引力势能的增加量。
假定光子到达无穷远处的频率为
，，引力质量为m，，光子的初始引力质量为m，
则有：
，
可得：
。
<<意味着光子能量的相对变化量很小，故从第三问可知：
继而可做如下推演：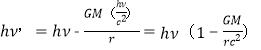
；
则有：
对于从半径为R的星球表面发射的光子，便有
由此可求得该星球的质量
