题目内容
18.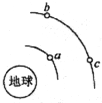 如图所示,a、b、c是地球大气层外圆形轨道上运动的三颗卫星,且b和c在同一个轨道上,则下列说法正确的是( )
如图所示,a、b、c是地球大气层外圆形轨道上运动的三颗卫星,且b和c在同一个轨道上,则下列说法正确的是( )| A. | b、c的周期相同,且大于a的周期 | |
| B. | b、c的线速度大小相等,且大于a的线速度 | |
| C. | b加速后可以实现与c对接 | |
| D. | a的线速度一定小于第一宇宙速度 |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、周期和向心力的表达式进行讨论即可.
解答 解:卫星绕地球做圆周运动,万有引力提供向心力;
A、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,由于ra<rb=rc,则:Ta<Tb=Tc,故A正确;
B、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,由于ra<rb=rc,则:va>vb=vc,故B错误;
C、b加速后做圆周运动需要的向心力变大,所需向心力小于在该轨道上受到的万有引力,b做离心运动,轨道半径变大,不可能与c对接,故C错误;
D、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,由于a的轨道半径大于地球半径,则a的线速度小于第一宇宙速度,故D正确;
故选:AD.
点评 本题考查了万有引力定律的应用,能根据万有引力提供圆周运动向心力并由此分析描述圆周运动的物理量与半径的关系是正确解题的关键.

练习册系列答案
相关题目
6.下列关于质点的说法正确的是( )
| A. | 只要物体运动不是很快,就可以把物体看作质点 | |
| B. | 体积很小的物体可以看成是质点,而体积较大的物体不能看作质点 | |
| C. | 质点是把物体抽象成有质量而没有大小的点,实际生活中并不存在 | |
| D. | 做旋转运动的物体,一定不能看作质点 |
10.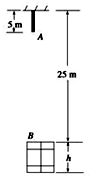 如图所示,有一根长L=5m的铁链悬挂在某楼顶上,楼中有一窗口,窗口上沿离铁链的悬点H=25m.当铁链从静止开始下落后始终保持竖直,不计空气阻力,g=10m/s2.则( )
如图所示,有一根长L=5m的铁链悬挂在某楼顶上,楼中有一窗口,窗口上沿离铁链的悬点H=25m.当铁链从静止开始下落后始终保持竖直,不计空气阻力,g=10m/s2.则( )
 如图所示,有一根长L=5m的铁链悬挂在某楼顶上,楼中有一窗口,窗口上沿离铁链的悬点H=25m.当铁链从静止开始下落后始终保持竖直,不计空气阻力,g=10m/s2.则( )
如图所示,有一根长L=5m的铁链悬挂在某楼顶上,楼中有一窗口,窗口上沿离铁链的悬点H=25m.当铁链从静止开始下落后始终保持竖直,不计空气阻力,g=10m/s2.则( )| A. | 铁链的下端A下落到窗口的上沿B时,铁链的速度大小为20m/s | |
| B. | 接着铁链经过整个窗口用了t=0.3s的时间,窗口的高度h为0.45m | |
| C. | 若升高悬点的高度,铁链经过整个窗口所用时间变长 | |
| D. | 若升高悬点的高度,铁链经过整个窗口所用时间变短 |
7.一平行板电容器C的极板是水平放置的,它和四个可变电阻及电源(电源内有内阻)连接成如图所示的电路,今有一质量为m的带正电油滴悬浮在两极板之间静止不动,现调节其中一个电阻,其余电阻不变,则( )

| A. | 若增大R1,油滴加速上升 | B. | 若增大R2,油滴加速上升 | ||
| C. | 若增大R3,油滴加速上升 | D. | 若增大R4,油滴加速上升 |
11.如图所示,甲、乙、丙、丁四幅图中,四个相同的磁体都处于静止状态,则( )
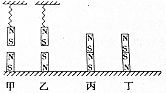

| A. | 对地面压力最大的是丙 | B. | 对地面压力最大的是甲 | ||
| C. | 对地面压力最大的是甲、丙、丁 | D. | 对地面压力最大的是丙、丁 |
 一长木板在水平地面上运动,在t=0时刻将一相对于地面静止的物块轻放到木板上,以后物块运动的速度-时间图象如图所示.己知物块与木板的质量相等,物块与木板间及木板与地面间均有摩擦,物块与木板间的最大静摩擦力等于滑动摩擦力,经0.5s木板前进S0=1.5m,且物块始终在木板上.取重力加速度的大小g=10m/s2,求:
一长木板在水平地面上运动,在t=0时刻将一相对于地面静止的物块轻放到木板上,以后物块运动的速度-时间图象如图所示.己知物块与木板的质量相等,物块与木板间及木板与地面间均有摩擦,物块与木板间的最大静摩擦力等于滑动摩擦力,经0.5s木板前进S0=1.5m,且物块始终在木板上.取重力加速度的大小g=10m/s2,求: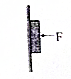 如图所示,重为G=10N的木块,被大小为F=40N的水平力压紧在竖直墙面上.木块静止,木块与墙面的动摩擦因素为μ=0.5.问:
如图所示,重为G=10N的木块,被大小为F=40N的水平力压紧在竖直墙面上.木块静止,木块与墙面的动摩擦因素为μ=0.5.问: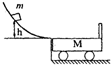 如图所示,光滑斜槽水平末端与停在光滑水平面上长为L=2.0m的小车上表面在同一水平面上,小车右端固定一个弹性挡板(即物体与挡板碰撞时无机械能损失).一个质量为m=1.0kg的小物块从斜槽上高h=1.25m处由静止滑下冲上小车,已知小车质量M=3.0kg,物块与小车间动摩擦因数为μ=0.45,g取l0m/s2.求整个运动过程中小车的最大速度.
如图所示,光滑斜槽水平末端与停在光滑水平面上长为L=2.0m的小车上表面在同一水平面上,小车右端固定一个弹性挡板(即物体与挡板碰撞时无机械能损失).一个质量为m=1.0kg的小物块从斜槽上高h=1.25m处由静止滑下冲上小车,已知小车质量M=3.0kg,物块与小车间动摩擦因数为μ=0.45,g取l0m/s2.求整个运动过程中小车的最大速度. 如图所示,在光滑绝缘平面上有A、B两个点电荷相距无穷远.A的质量为m,且静止;B的质量为4m,且以速度v正对着A运动.则运动过程中A、B系统具有最大电势能为0.4mv2.
如图所示,在光滑绝缘平面上有A、B两个点电荷相距无穷远.A的质量为m,且静止;B的质量为4m,且以速度v正对着A运动.则运动过程中A、B系统具有最大电势能为0.4mv2.