题目内容
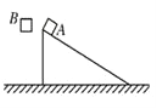
【题目】如图A.所示,质量为60 kg的消防队员从一根固定的竖直金属杆上由静止滑下,经2.5 s落地。消防队员下滑过程中的速度随时间的变化如图B.所示。取g=10 m/s2,求:
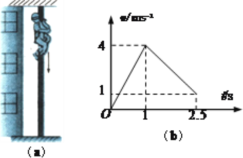
(1)消防员在加速下滑和减速下滑时受到的摩擦力f1和f2;
(2)他下滑的高度H;
(3)他克服摩擦力做的总功W。
【答案】(1)360N, 720N(2)5.75m(3)3420J
【解析】
(1)根据v-t图像先求解下滑加速和减速阶段的加速度,根据牛顿第二定律求解摩擦力;(2)根据位移时间关系式求解下落的高度;(3)根据功的概念求解摩擦力的功.
(1)根据图(a)可知:该消防员加速时的加速度a1=![]() =4m/s2;
=4m/s2;
减速时加速度的a2=![]() =2m/s2
=2m/s2
消防员下滑过程在竖直方向受到重力和竖直向上的摩擦力作用。
设加速度下滑时受到的摩擦力为f1,减速下滑时受到的摩擦力为f2
根据牛顿第二定律有 ma1=mg- f1;-ma2=mg- f2
可求得: f1=360N,f2=720N
(2)设他加速下滑的高度为h1、减速下滑的高度为h2,根据匀变速运动规律有
h1=![]() a1t12=
a1t12=![]() ×4×12 m =2m
×4×12 m =2m
h2= v t2 - ![]() a2t22=(4×1.5 -
a2t22=(4×1.5 -![]() ×2×1.52)m=3.75m
×2×1.52)m=3.75m
所以他下落的高度 H= h1+ h2=5.75m
(3)加速下滑过程中,克服摩擦力做功:W1= f1 h1=360×2J=720J
减速下滑过程中,克服摩擦力做功:W2= f2 h2=720×3.75J=2700J
在整个下滑过程中他一共克服摩擦力做功:W= W1+ W2=3420J

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目