题目内容
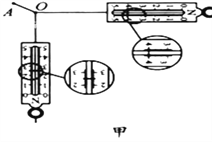
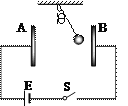
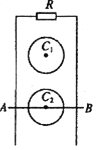
【题目】如图所示,竖直光滑导轨上端接入一定值电阻R,C1和C2是半径都为a的两圆形磁场区域,其区域内的磁场方向都垂直于导轨平面向外,区域C1中磁场的磁感应强度随时间接B1=b+kt (k>0)变化,C2中磁场的磁感应强度恒为B2,一质量为m.电阻为r、长度为L的金属杆AB穿过C2的圆心垂直地跨放在两导轨上,且与导轨接触良好,并恰能保持静止。则
A. 通过金属杆的电流大小为![]()
B. 通过金属杆的电流方向为从B到A
C. 定值电阻的阻值为R=![]()
D. 整个电路的热功率p=![]()
【答案】BCD
【解析】试题分析:金属杆静止,合力为零.根据受力分析,结合平衡条件与安培力表达式,求解通过金属杆的电流大小;由楞次定律分析通过金属杆的电流方向.根据法拉第电磁感应定律与闭合电路欧姆定律,结合题意,即可求定值电阻的阻值.由功率公式整个电路中产生的热功率P.
对金属杆,根据平衡方程得![]() ,解得
,解得![]() ,故A错误;区域C1中磁场的磁感强度随时间按B1=b+kt(k>0)变化,可知磁感强度均匀增大,穿过整个回路的磁通量增大,由楞次定律分析知,通过金属杆的电流方向为从B到A,B正确;由法拉第电磁感应定律,则有:回路中产生的感应电动势为
,故A错误;区域C1中磁场的磁感强度随时间按B1=b+kt(k>0)变化,可知磁感强度均匀增大,穿过整个回路的磁通量增大,由楞次定律分析知,通过金属杆的电流方向为从B到A,B正确;由法拉第电磁感应定律,则有:回路中产生的感应电动势为![]() ,且闭合电路欧姆定律有
,且闭合电路欧姆定律有![]() ,又
,又![]() ,解得
,解得![]() ,C正确;整个电路中产生的热功率
,C正确;整个电路中产生的热功率![]() ,D正确.
,D正确.

练习册系列答案
相关题目