��Ŀ����
����Ŀ����ΪL�ľ�Եϸ����ϵһ�������С����������ΪQ������Ϊm�������컨���ϵ�O������ͼ��ʾ��������O�㴦�̶�һ������Ϊ�ʵ�Ĵ���������壬��ֹ��O�����·�A��ʱ������������������mg���������ֽ�������ͼ��B������=60���������ͷţ�ʹ������ֱ�������ذڶ������ʣ�
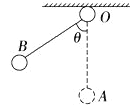
��1��O�㴦������ĵ�����Ƕ��٣�
��2����ڻص�A��ʱ���ߵ�����Ϊ�����
���𰸡���1��![]() ��2��T=3mg
��2��T=3mg
�������������������ֹ��A������������֪�����������ã�������������F��ϸ��������������ƽ��Ϳ��ض�����ʽ��⣻�ڻصĹ���ֻ���������������Ի�е���غ㣬�г���ʽ��ʾ����͵��ٶȣ���ţ�ٵڶ�������⣮
��1����O��̶���ɵĵ���Ϊq��Q��ֹ��A��ʱ��������ƽ�������ã� ![]()
��![]() ������ʽ����
������ʽ����![]() ��
��
��2������A��ʱ���ٶ�Ϊ![]() ������B��A�������뾲��������������е���غ㡣���У�
������B��A�������뾲��������������е���غ㡣���У� ![]() ��
��
����ڻ�A��ʱ��������ΪT��������������ʽ�ã� ![]() ��
��
����٢ڢ�ʽ����![]()

��ϰ��ϵ�д�
 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
�����Ŀ