题目内容
1.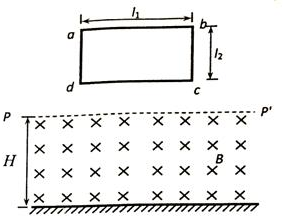 如图所示,水平地面上方的H高区域内均有匀强磁场,水平界面PP′是磁场的上边界,磁感应强度为B=1T,方向是水平的,垂直于纸面向里.在磁场的正上方,有一个位于竖直平面内的闭合的矩形平面导线框abcd,ab长为l1=1m,bc长为l2=0.5m,H=2.7m,线框的质量为m=1kg,电阻为R=1Ω.使线框abcd从高处自由落下,ab边下落的过程中始终保持水平,已知线框进入磁场的过程中的运动情况是:cd边进入磁场以后,线框先做加速运动,然后做匀速运动,直到ab边到达边界PP′为止.从线框开始下落到cd边刚好到达水平地面的过程中,线框中产生的焦耳热为Q=10J.g=10m/s2求:
如图所示,水平地面上方的H高区域内均有匀强磁场,水平界面PP′是磁场的上边界,磁感应强度为B=1T,方向是水平的,垂直于纸面向里.在磁场的正上方,有一个位于竖直平面内的闭合的矩形平面导线框abcd,ab长为l1=1m,bc长为l2=0.5m,H=2.7m,线框的质量为m=1kg,电阻为R=1Ω.使线框abcd从高处自由落下,ab边下落的过程中始终保持水平,已知线框进入磁场的过程中的运动情况是:cd边进入磁场以后,线框先做加速运动,然后做匀速运动,直到ab边到达边界PP′为止.从线框开始下落到cd边刚好到达水平地面的过程中,线框中产生的焦耳热为Q=10J.g=10m/s2求:(1)线框abcd在进入磁场的过程中,通过导线的某一横截面的电荷量是多少?
(2)线框是从cd边距边界PP′多高处开始下落的?
(3)线框的cd边到达地面时线框的速度大小是多少?
分析 (1)由法拉第电磁感应定律求出感应电动势,然后由欧姆定律与电流的定义式求出电荷量.
(2)当重力等于安培力时,线框做匀速运动,根据安培力公式与平衡条件可求出匀速运动的速度.从线框开始下落到cd边刚好到达水平地面的过程中,线框的重力势能减小转化为线框的动能和内能,根据能量守恒定律求解高度.
(3)线框的ab边进入磁场后,只有重力作用下,线框做匀加速运动,由运动学公式求解线框的cd边到达地面时线框的速度大小.
解答 解:(1)由法拉第电磁感应定律得:$\overline{E}$=$\frac{△Φ}{△t}$=$\frac{B{l}_{1}{l}_{2}}{△t}$,
感应电流:$\overline{I}$=$\frac{\overline{E}}{R}$=$\frac{B{l}_{1}{l}_{2}}{R△t}$$\frac{B{l}_{1}{l}_{2}}{R}$,
通过导线的某一横截面的电荷量:q=$\overline{I}$△t=$\frac{B{l}_{1}{l}_{2}}{R}$,
解得:q=0.5C;
(2)设线框从cd边距边界PP′上方h高处开始下落,cd边进入磁场后,
切割磁感线,产生感应电流,在安培力作用下做加速度逐渐减小的加速运动,
直到安培力等于重力后匀速下落,速度设为v,匀速过程一直持续到ab边进入磁场时结束,
有:E=Bl1v,I=$\frac{E}{R}$,安培力:FA=BIl1=$\frac{{B}^{2}{l}_{1}^{2}v}{R}$,线框匀速运动,由平衡条件得:FA=mg,
即:mg=$\frac{{B}^{2}{l}_{1}^{2}v}{R}$,
解得:v=10m/s,
线框的ab边进入磁场后,线框中没有感应电流.只有在线框进入磁场的过程中有焦耳热Q.
线框从开始下落到ab边刚进入磁场的过程中,线框的重力势能转化为线框的动能和电路中的焦耳热.
由能量守恒定律得:mg(h+l2)=$\frac{1}{2}$mv2+Q,
解得:h=5.5m;
(3)线框的ab边进入磁场后,只有重力作用下,匀加速下落,加速度大小为g,
则有:v12-v2=2g(H-l2),解得,cd边到达地面时线框的速度:v1=12m/s;
答:(1)线框abcd在进入磁场的过程中,通过导线的某一横截面的电荷量是0.5C;
(2)线框是从cd边距边界PP′5.5m高处开始下落的;
(3)线框的cd边到达地面时线框的速度大小是12m/s.
点评 本题是电磁感应与力学、电学相结合的综合题,分析清楚物体的运动过程是解题的关键,应用法拉第电磁感应定律、欧姆定律、安培力公式、能量守恒定律可以解题.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案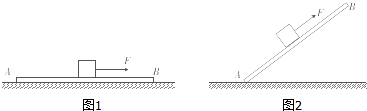
| A. | $\frac{3}{4}$F | B. | F | C. | 2F | D. | $\frac{11}{5}$F |

| A. | 电动势E1=E2,发生短路时的电流I1>I2 | |
| B. | 电动势E1=E2,内阻r1<r2 | |
| C. | 电动势E1>E2,内阻 r1<r2 | |
| D. | 当两电源的工作电流变化量相同时,电源2的路端电压变化大 |
| A. | 9 m | B. | 12 m | C. | 21 m | D. | 8 m |
| A. | 摩擦起电,说明了机械能可以转化为电能,也说明通过做功可以创造电荷 | |
| B. | 任何物体所带的电荷量只能是某些特定的值 | |
| C. | 库仑创造性地在电场中引入电场线,用它来形象化的描述电荷周围的电场 | |
| D. | 要使真空中的两个点电荷间的库仑力增大到原来的4倍,则要使每个点电荷的电荷量都增大到原来的2倍,电荷间的距离变为原来的$\frac{1}{2}$ |
 某实验小组用如图1所示实验电路测三节干电池组成的电池组的电动势和内阻,定值电阻3Ω.
某实验小组用如图1所示实验电路测三节干电池组成的电池组的电动势和内阻,定值电阻3Ω. 如图所示,重物用BC、AC、CD三根绳吊在天花板上,已知β=30°,α=60°,BC和AC所能承受的最大拉力均为100N,CD能承受的最大拉力为300N,若使三根绳均不断,则挂在下面的物体的重力不能超过多大?
如图所示,重物用BC、AC、CD三根绳吊在天花板上,已知β=30°,α=60°,BC和AC所能承受的最大拉力均为100N,CD能承受的最大拉力为300N,若使三根绳均不断,则挂在下面的物体的重力不能超过多大?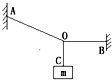 如图所示,一个悬挂重物的系统,其中AO、BO、CO都是最多能承受100N的细绳,已知BO处于水平位置,∠AOB为150°.欲使绳子不致断裂,所悬挂的重物m的重力不能超过多少?
如图所示,一个悬挂重物的系统,其中AO、BO、CO都是最多能承受100N的细绳,已知BO处于水平位置,∠AOB为150°.欲使绳子不致断裂,所悬挂的重物m的重力不能超过多少?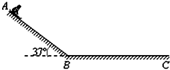 在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡的高处A点由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,人在斜坡上滑下的距离AB=3m,滑板与斜坡摩擦忽略不计,滑板与水平滑道间的动摩擦因数μ=0.10,斜坡的倾角θ=37°.斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计.求:
在海滨游乐场里有一种滑沙的游乐活动.如图所示,人坐在滑板上从斜坡的高处A点由静止开始滑下,滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来.若某人和滑板的总质量m=60.0kg,人在斜坡上滑下的距离AB=3m,滑板与斜坡摩擦忽略不计,滑板与水平滑道间的动摩擦因数μ=0.10,斜坡的倾角θ=37°.斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计.求: