题目内容
9.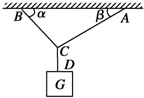 如图所示,重物用BC、AC、CD三根绳吊在天花板上,已知β=30°,α=60°,BC和AC所能承受的最大拉力均为100N,CD能承受的最大拉力为300N,若使三根绳均不断,则挂在下面的物体的重力不能超过多大?
如图所示,重物用BC、AC、CD三根绳吊在天花板上,已知β=30°,α=60°,BC和AC所能承受的最大拉力均为100N,CD能承受的最大拉力为300N,若使三根绳均不断,则挂在下面的物体的重力不能超过多大?
分析 结点C为研究对象作出受力分析图,分析BC、AC两绳拉力的大小,确定哪根绳子的拉力先达到最大.再根据受力平衡列方程解得结果.
解答  解:以C点为研究对象,重物对结点的拉力等于重物的重力:TC=G,分析C点受力如图.
解:以C点为研究对象,重物对结点的拉力等于重物的重力:TC=G,分析C点受力如图.
由平衡条件和几何关系可得:
FTB=Gcos30°=$\frac{\sqrt{3}}{2}$GA;
FTA=Gsin30°=$\frac{1}{2}G$B;
由题知:FTAmax=100N,FTBmax=100N,FTCmax=300N,
当FTAmax=100N时,由上解得 GA=200N
当FTBmax=100N时,由上解得 GB=$\frac{200}{3}\sqrt{3}$N
当FTCmax=300N时,GC=300N
故随着重物重力的增加,BC最先断开,故重力最大不超过$\frac{200}{3}\sqrt{3}$N.
答:挂在下面的物体的重力不能超过$\frac{200}{3}\sqrt{3}$N.
点评 本题是静力学中临界问题,分析临界条件是关键.当绳子刚要被拉断时,绳子的拉力达到最大值,是常用的临界条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.关于质点,下列说法中正确的是( )
| A. | 研究“神舟十号”飞船绕地球飞行的轨道时,飞船不可以看成质点 | |
| B. | 计算火车通过南京长江大桥的时间,火车可以看成质点 | |
| C. | 研究体操运动员在空中的动作时,运动员可以看成质点 | |
| D. | 质点是为了研究问题方便而建立的理想化模型 |
14.如图甲所示,足够长的木板B静置于光滑水平面上,其上放置小滑块A.木板B受到随时间t变化的水平拉力F作用时,用传感器测出木板B的加速度a,得到如图乙所示的a-F图象,已知g取10m/s2,则( )


| A. | 滑块A的质量为4kg | B. | 木板B的质量为1kg | ||
| C. | 当F=10N时木板B加速度为4m/s2 | D. | 滑块A与木板B间动摩擦因数为0.1 |
18.当小强荡到最低点时( )
| A. | 若角速度一定,则绳短时绳受到的拉力大 | |
| B. | 若线速度一定,则绳长时绳受到的拉力大 | |
| C. | 若角速度一定,则绳长时绳受到的拉力大 | |
| D. | 绳受到的拉力大小始终等于小强的重力 |
19.以下的计时数据指时间间隔的是( )
| A. | 从北京开往西安的火车预计13点到 | |
| B. | 中央电视台每晚的新闻联播节目19点开播 | |
| C. | 某足球赛伤停补时3min | |
| D. | 1997年7月1号香港回归祖国 |
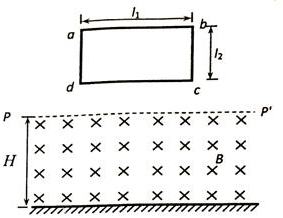 如图所示,水平地面上方的H高区域内均有匀强磁场,水平界面PP′是磁场的上边界,磁感应强度为B=1T,方向是水平的,垂直于纸面向里.在磁场的正上方,有一个位于竖直平面内的闭合的矩形平面导线框abcd,ab长为l1=1m,bc长为l2=0.5m,H=2.7m,线框的质量为m=1kg,电阻为R=1Ω.使线框abcd从高处自由落下,ab边下落的过程中始终保持水平,已知线框进入磁场的过程中的运动情况是:cd边进入磁场以后,线框先做加速运动,然后做匀速运动,直到ab边到达边界PP′为止.从线框开始下落到cd边刚好到达水平地面的过程中,线框中产生的焦耳热为Q=10J.g=10m/s2求:
如图所示,水平地面上方的H高区域内均有匀强磁场,水平界面PP′是磁场的上边界,磁感应强度为B=1T,方向是水平的,垂直于纸面向里.在磁场的正上方,有一个位于竖直平面内的闭合的矩形平面导线框abcd,ab长为l1=1m,bc长为l2=0.5m,H=2.7m,线框的质量为m=1kg,电阻为R=1Ω.使线框abcd从高处自由落下,ab边下落的过程中始终保持水平,已知线框进入磁场的过程中的运动情况是:cd边进入磁场以后,线框先做加速运动,然后做匀速运动,直到ab边到达边界PP′为止.从线框开始下落到cd边刚好到达水平地面的过程中,线框中产生的焦耳热为Q=10J.g=10m/s2求: