题目内容
走时准确的机械手表的时针、分针、秒针都在匀速转动,A、B、C分别是时针、分针、秒针针尖上的点,则以下比例关系正确的是( )A.A、B、C三点做圆周运动的周期之比为1:60:3600
B.A、B、C三点做圆周运动的周期之比为3600:60:1
C.A、B、C三点做圆周运动的角速度之比为1:12:720
D.A、B、C三点做圆周运动的角速度之比为720:12:1
【答案】分析:解决本题的关键正确理解周期定义,然后利用周期和角速度的关系ω=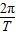 求解角速度.
求解角速度.
解答:解:时针运动的周期为12h,故时针上的A点做圆周运动的周期为T1=12h,
而分针运动一周需要1h,故分针上的B点做圆周运动的周期为T2=1h,
秒针绕圆心运动一周需要60s,故秒针上的C点做圆周运动的周期为T3=60s=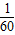 h,
h,
故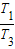 =
=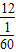 =
=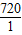
同理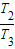 =
=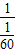 =
=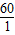
∴A、B、C三点做圆周运动的周期之比为T1:T2:T3=720:60:1
根据物体做圆周运动的周期和角速度之间的关系式ω=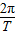
可得A点做圆周运动的角速度ω1=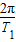
B点做圆周运动的角速度ω2=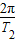
C点做圆周运动的角速度ω3=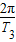
所以ω1:ω2=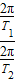 =
=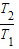 =
=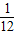
同理ω1:ω3=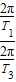 =
=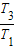 =
=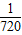
∴ω1:ω2:ω3=1:12:720
故选C.
点评:解决本题的关键是要正确把握机械表的三个指针转动的周期,并能熟练应用周期和角速度的关系.
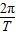 求解角速度.
求解角速度.解答:解:时针运动的周期为12h,故时针上的A点做圆周运动的周期为T1=12h,
而分针运动一周需要1h,故分针上的B点做圆周运动的周期为T2=1h,
秒针绕圆心运动一周需要60s,故秒针上的C点做圆周运动的周期为T3=60s=
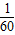 h,
h,故
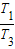 =
=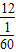 =
=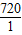
同理
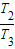 =
=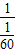 =
=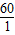
∴A、B、C三点做圆周运动的周期之比为T1:T2:T3=720:60:1
根据物体做圆周运动的周期和角速度之间的关系式ω=
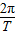
可得A点做圆周运动的角速度ω1=
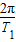
B点做圆周运动的角速度ω2=
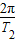
C点做圆周运动的角速度ω3=
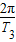
所以ω1:ω2=
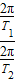 =
=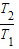 =
=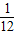
同理ω1:ω3=
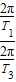 =
=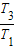 =
=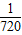
∴ω1:ω2:ω3=1:12:720
故选C.
点评:解决本题的关键是要正确把握机械表的三个指针转动的周期,并能熟练应用周期和角速度的关系.

练习册系列答案
相关题目