题目内容
 (2012?盐城三模)如图所示,空间存在一个半径为R0的圆形匀强磁场区域,磁场的方向垂直于纸面向里,磁感应强度的大小为B.有一个粒子源在纸面内沿各个方向以一定速率发射大量粒子,粒子的质量为m、电荷量为+q.将粒子源置于圆心,则所有粒子刚好都不离开磁场,不考虑粒子之间的相互作用.
(2012?盐城三模)如图所示,空间存在一个半径为R0的圆形匀强磁场区域,磁场的方向垂直于纸面向里,磁感应强度的大小为B.有一个粒子源在纸面内沿各个方向以一定速率发射大量粒子,粒子的质量为m、电荷量为+q.将粒子源置于圆心,则所有粒子刚好都不离开磁场,不考虑粒子之间的相互作用.(1)求带电粒子的速率.
(2)若粒子源可置于磁场中任意位置,且磁场的磁感应强度大小变为
| B |
| 4 |
(3)若原磁场不变,再叠加另一个半径为R1(R1>R0)圆形匀强磁场,磁场的磁感应强度的大小为
| B |
| 2 |
分析:(1)根据几何关系,结合洛伦兹力提供向心力,由牛顿第二定律,即可求解;
(2)由几何关系,可求出运动轨迹的圆心角,根据周期公式,即可求解;
(3)根据矢量法则,可确定磁场方向与大小,再由几何关系,结合周期公式,即可求解.
(2)由几何关系,可求出运动轨迹的圆心角,根据周期公式,即可求解;
(3)根据矢量法则,可确定磁场方向与大小,再由几何关系,结合周期公式,即可求解.
解答: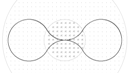 解:(1)粒子离开出发点最远的距离为轨道半径的2倍
解:(1)粒子离开出发点最远的距离为轨道半径的2倍
几何关系,则有R0=2r=
根据半径公式,解得v=
(2)磁场的大小变为
后,粒子的轨道半径为2R0,
根据几何关系可以得到,当弦最长时,运动的时间最长,弦为2 R0时最长,圆心角60°
解得:t=
T=
(3)根据矢量合成法则,叠加区域的磁场大小为
,方向向里,
R0以为的区域磁场大小为
,方向向外.粒子运动的半径为R0,
根据对称性画出情境图,由几何关系可得R1的最小值为(
+1)R0
T=
=
答:(1)求带电粒子的速率得v=
.
(2)若粒子源可置于磁场中任意位置,且磁场的磁感应强度大小变为
,则粒子在磁场中最长的运动时间
.
(3)若原磁场不变,再叠加另一个半径为R1(R1>R0)圆形匀强磁场,磁场的磁感应强度的大小为
,方向垂直于纸面向外,两磁场区域成同心圆,此时该离子源从圆心出发的粒子都能回到圆心,则R1的最小值和粒子运动的周期
.
 解:(1)粒子离开出发点最远的距离为轨道半径的2倍
解:(1)粒子离开出发点最远的距离为轨道半径的2倍几何关系,则有R0=2r=
| 2mv |
| Bq |
根据半径公式,解得v=
| qBR0 |
| 2m |
(2)磁场的大小变为
| B |
| 4 |
根据几何关系可以得到,当弦最长时,运动的时间最长,弦为2 R0时最长,圆心角60°
解得:t=
| 60° |
| 360° |
| 4πm |
| 3qB |
(3)根据矢量合成法则,叠加区域的磁场大小为
| B |
| 2 |
R0以为的区域磁场大小为
| B |
| 2 |
根据对称性画出情境图,由几何关系可得R1的最小值为(
| 3 |
T=
(
| ||||
q
|
| 28πm |
| 3qB |
答:(1)求带电粒子的速率得v=
| qBR0 |
| 2m |
(2)若粒子源可置于磁场中任意位置,且磁场的磁感应强度大小变为
| B |
| 4 |
| 4πm |
| 3qB |
(3)若原磁场不变,再叠加另一个半径为R1(R1>R0)圆形匀强磁场,磁场的磁感应强度的大小为
| B |
| 2 |
| 28πm |
| 3qB |
点评:洛伦兹力提供圆周运动向心力,根据轨迹关系求出粒子进入磁场中的速度方向,再根据速度关系求出质子在电场中做何种运动,然后根据运动性质求解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 (2012?盐城三模)如图所示,置于竖直平面内的AB光滑杆,它是以初速为v0,水平射程为s的平抛运动轨迹制成的,A端为抛出点,B端为落地点.现将一小球套于其上,由静止开始从轨道A端滑下,重力加速度为g.则当其到达轨道B端时( )
(2012?盐城三模)如图所示,置于竖直平面内的AB光滑杆,它是以初速为v0,水平射程为s的平抛运动轨迹制成的,A端为抛出点,B端为落地点.现将一小球套于其上,由静止开始从轨道A端滑下,重力加速度为g.则当其到达轨道B端时( ) (2012?盐城三模)如图所示,光滑绝缘水平桌面上有A、B两个带电小球(可以看成点电荷),A球带电量为+2q,B球带电量为-q,将它们同时由静止开始释放,A球加速度的大小为B球的2倍.现在AB中点固定一个带电小球C(也可看作点电荷),再同时由静止释放A、B两球,释放瞬间两球加速度大小相等.则C球带电量可能为( )
(2012?盐城三模)如图所示,光滑绝缘水平桌面上有A、B两个带电小球(可以看成点电荷),A球带电量为+2q,B球带电量为-q,将它们同时由静止开始释放,A球加速度的大小为B球的2倍.现在AB中点固定一个带电小球C(也可看作点电荷),再同时由静止释放A、B两球,释放瞬间两球加速度大小相等.则C球带电量可能为( )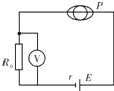 (2012?盐城三模)酒精测试仪的工作电路可简化为如图所示,其中P是半导体型酒精气体传感器,该传感器电阻RP与酒精气体的浓度c成反比,R0为定值电阻.电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
(2012?盐城三模)酒精测试仪的工作电路可简化为如图所示,其中P是半导体型酒精气体传感器,该传感器电阻RP与酒精气体的浓度c成反比,R0为定值电阻.电压表示数U与酒精气体浓度c之间的对应关系正确的是( )