Question

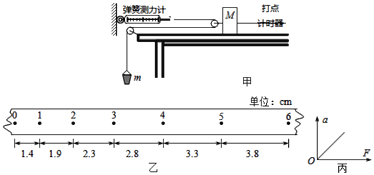
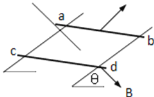
【题目】如图所示，一质量＝的小物块，以＝的初速度，在与斜面成某一夹角的拉力作用下，沿斜面向上做匀加速运动，经＝的时间物块由点运动到点，、之间的距离＝。已知斜面倾角＝，物块与斜面之间的动摩擦因数．重力加速度取。

（1）求物块加速度的大小及到达点时速度的大小；

（2）拉力与斜面夹角多大时，拉力最小？拉力的最小值是多少？

Answer 1

【答案】（1）；（2），

【解析】

(1)设物块加速度的大小为a，到达B点时速度的大小为v，由运动学公式得：

，

代入数据得：

a=3m/s2，v=8m/s

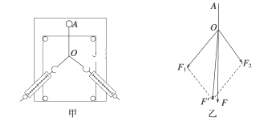
(2) 设物块所受支持力为FN，所受摩擦力为Ff，拉力与斜面间的夹角为α，受力分析如图所示

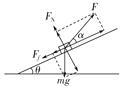
由牛顿第二定律得：

Fcosα-mgsinθ-Ff=ma，Fsinα+FN-mgcosθ=0，Ff=μFN

联立得

由数学知识得：

可知对应最小F的夹角

α=30°

代入数据得F的最小值为：