题目内容
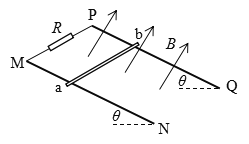
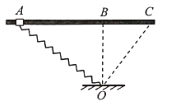
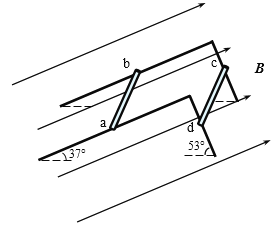
【题目】如图所示，固定的直角金属轨道足够长，左侧倾角θ1=37°，右侧倾角θ2=53°，轨道宽均为L=1.0m，整个装置处于B=1.0T匀强磁场中，磁场方向垂直于右侧轨道平面向上。质量分别为m1=1.0kg、m2=0.4kg的导体棒ab、cd，水平放在左、右两侧轨道上并与轨道垂直。已知ab、cd棒的电阻均为R=1.0Ω，其余电阻不计，两棒与轨道间的动摩擦因数均为μ=0.5，最大静摩擦力等于滑动摩擦力，重力加速度g取10m/s2，sin37°=0.6，sin53°＝0.8。由静止同时释放两棒，在棒下滑过程中
（1）判断cd棒中感应电流的方向；
（2）通过分析说明cd棒下滑过程中的运动情况，并计算ab棒中电功率的最大值；
（3）通过分析、推理和计算，说明ab棒在下滑过程中的运动情况。
【答案】（1）沿cd方向（2）做加速度逐渐减小的加速运动，4.0W（3）见解析
【解析】
（1）cd棒下滑切割磁感线，ab棒下滑不切割磁感线，根据右手定则，在cd棒中I沿cd方向。
（2）cd棒在右侧轨道上受力情况如图所示
f2=μN2=μm2gcos53°=0.5×0.4×10×0.6N=1.2N
由牛顿第二定律得
m2gsin53°-f2-FA2=m2a2
FA2=BIL=
v增大，a2减小，cd棒做加速度逐渐减小的加速运动
当FA2==m2gsin53°-f2=（0.4×10×0.8-1.2）N=2.0N时速度最大
此后cd棒以最大速度匀速运动，最大电流
Im=
=2.0A
ab棒最大电功率
Pm=Im2R=4.0W
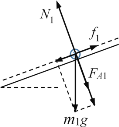
（3）ab棒在左侧轨道上受力情况如图
ab棒刚释放时
m1gsin37°=6N
最大静摩擦力
fmax=μN1=μm1gcos37°=0.5×1×10×0.8N=4N
因为fmax<m1gsin37°
所以刚释放时ab棒沿斜面向下加速运动
N1=FA1+m1gcos37°=+m1gcos37°
f1=μN1=μ（+m1gcos37°）
由牛顿第二定律得
m1gsin37°-f1=m1gsin37°-μ（+m1gcos37°）=m1a1
当cd棒下滑速度v增大时，a1减小，棒ab做加速度逐渐减小的加速运动
当cd棒速度达到最大后，Im=2A不变
f1m=μ（m1gcos37°+BImL）=5N<m1gsin37°=6N
ab棒开始做加速度为a1=（m1gsin37°-f1m）/m1=1m/s2的匀加速直线运动
名师点睛字词句段篇系列答案
【题目】某研究性学习小组欲测定一块电池的电动势 E。用电压表 V、电阻箱 R、定值电阻 R0 、开关 S、若干导线和该电池组成电路，测定该电池电动势。
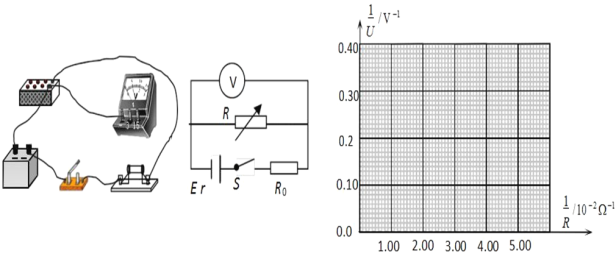
(1)根据电路图，用笔画线代替导线，将实物图连接成完整电路。（__________）
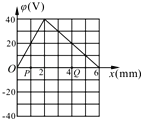
(2)闭合开关 S，调整电阻箱阻值 R，读出电压表 V 相应示数 U。该学习小组测出大量数据，分析筛选出下表所示的 R、U 数据，并计算出相应的 
与
的值。请用表中数据在坐标纸上描点，并作出 -- 图线。（__________）
R（Ω） | 166.7 | 71.4 | 50.0 | 33.3 | 25.0 | 20.0 |
U（V ） | 8.3 | 5.9 | 4.8 | 4.2 | 3.2 | 2.9 |
| 0.60 | 1.40 | 2.00 | 3.00 | 4.00 | 5.00 |
| 0.12 | 0.17 | 0.21 | 0.24 | 0.31 | 0.35 |
(3)从图线中可以求得电动势 E=_______V（结果保留两位有效数字）。
