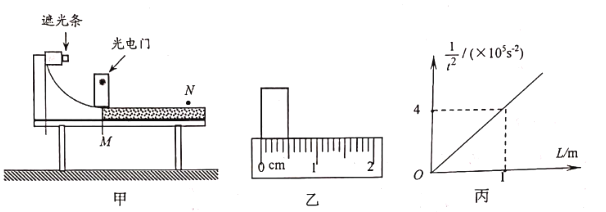
题目内容
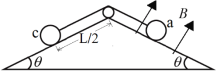
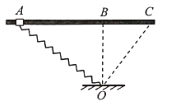
【题目】如图所示,粗糙的固定水平杆上有![]() 三点,轻质弹簧一端固定在
三点,轻质弹簧一端固定在![]() 点正下方的
点正下方的![]() 点,另一端与套在杆
点,另一端与套在杆![]() 点、质量为
点、质量为![]() 的圆环相连,此时弹簧处于拉伸状态。圆环从
的圆环相连,此时弹簧处于拉伸状态。圆环从![]() 处由静止释放,向右运动经过
处由静止释放,向右运动经过![]() 点时速度为
点时速度为![]() 、加速度为零,到达
、加速度为零,到达![]() 点时速度为零,下列说法正确的是
点时速度为零,下列说法正确的是
A.从![]() 到
到![]() 过程中,圆环在
过程中,圆环在![]() 点速度最大
点速度最大
B.从![]() 到
到![]() 过程中,圆环的加速度先减小后增大
过程中,圆环的加速度先减小后增大
C.从![]() 到
到![]() 过程中,弹簧对圆环做的功一定大于
过程中,弹簧对圆环做的功一定大于![]()
D.从![]() 到
到![]() 过程中,圆环克服摩擦力做功等于
过程中,圆环克服摩擦力做功等于![]()
【答案】C
【解析】
AB.圆环由A点释放,此时弹簧处于拉伸状态,则圆环加速运动,设AB之间的D位置为弹簧的原长,则A到D的过程中,弹簧弹力减小,圆环的加速度逐渐减小,D到B的过程中,弹簧处于压缩状态,则弹簧弹力增大,圆环的加速度先增大后减小,B点时,圆环合力为零,竖直向上的弹力等于重力,从B到C的过程中,圆环可能做减速运动,无论是否存在弹簧原长的位置,圆环的加速度始终增大,也可能先做加速后做减速运动,加速度先减小后增大,故B点的速度不一定最大,从A到C过程中,圆环的加速度不是先减小后增大,故AB错误;
C.从A到B过程中,弹簧对圆环做的功、摩擦力做负功,根据功能关系可知,弹簧对圆环做功一定大于![]() ,故C正确;
,故C正确;
D.从B到C过程中,弹簧弹力做功,圆环克服摩擦力做功,根据功能关系可知,圆环克服摩擦力做功不等于![]() ,故D错误。
,故D错误。
故选C。

练习册系列答案
相关题目