��Ŀ����
����Ŀ����ͼ��ʾ�������δ��ʹ���1m/s���ٶ���ʱ������ת�������ߵĴ��ʹ�������2m����ˮƽ����ļнǾ�Ϊ37������������С���A��Bͬʱ�Ӵ��ʹ����˶���1m/s�ij��ٶ��ش��ʹ��»�����֪����봫�ʹ���Ķ�Ħ����������0��5��sin37��=0��6��cos37��=0��8���������ٶ�g=10m/s2������˵����ȷ������ ��
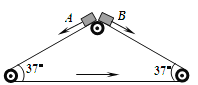
A�����A��B�˶��ļ��ٶȴ�С��ͬ
B�����A���ȵ��ﴫ�ʹ���
C�����A��B�˶������ʹ���ʱ�����Ĺ������
D�����A��B�ڴ��ʹ��ϵĻ��۳���֮��Ϊ1��3
���𰸡�D
��������
��������������������б�淽��������![]() ��������鶼����б�����»��������ʹ������AB��Ħ�������ش��ʹ����������Ҽ��ٶȴ�С������
��������鶼����б�����»��������ʹ������AB��Ħ�������ش��ʹ����������Ҽ��ٶȴ�С������![]() �����ٶ���ͬ�����ٶȴ�С��ͬ��������λ�ƴ�С��ͬ������
�����ٶ���ͬ�����ٶȴ�С��ͬ��������λ�ƴ�С��ͬ������![]() ��֪���ߵ��˶�ʱ����ͬ����Ϊ
��֪���ߵ��˶�ʱ����ͬ����Ϊ![]() ��������ͬʱ�������AB������Ħ�������ϣ�λ�����£�������������Ħ�������������������A��B�˶������ʹ���ʱ�ٶȵĴ�С��ͬ�������֪AB��ˮƽ��ļн�����ȵģ����������Ĺ���һ����ȣ���C��ȷ��B���ﴫ�ʹ���ʱ���ٶ�
��������ͬʱ�������AB������Ħ�������ϣ�λ�����£�������������Ħ�������������������A��B�˶������ʹ���ʱ�ٶȵĴ�С��ͬ�������֪AB��ˮƽ��ļн�����ȵģ����������Ĺ���һ����ȣ���C��ȷ��B���ﴫ�ʹ���ʱ���ٶ�![]() �����ʹ���1s�ڵ�·��Ϊ
�����ʹ���1s�ڵ�·��Ϊ![]() ��A�봫�ʹ���ͬ���˶��ģ�A�Ļ��۳�����A�Ե�·����б�泤������ȥ�ڴ�ʱ���ڴ��ʹ���·�̣���Ϊ
��A�봫�ʹ���ͬ���˶��ģ�A�Ļ��۳�����A�Ե�·����б�泤������ȥ�ڴ�ʱ���ڴ��ʹ���·�̣���Ϊ![]() ��B�봫�ʹ��Ƿ����˶��ģ�B�Ļ��۳�����B�Ե�·����б�泤���������ڴ�ʱ���ڴ��ʹ���·�̣���Ϊ
��B�봫�ʹ��Ƿ����˶��ģ�B�Ļ��۳�����B�Ե�·����б�泤���������ڴ�ʱ���ڴ��ʹ���·�̣���Ϊ ![]() �������A��B�ڴ��ʹ��ϵĻ��۳���֮��Ϊ1��3����D��ȷ��
�������A��B�ڴ��ʹ��ϵĻ��۳���֮��Ϊ1��3����D��ȷ��