题目内容
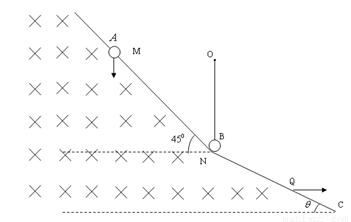
如图，虚线的左下方存在匀强磁场大小B。A、B是完全相同的两个质量均为m的小金属球(可看做质点)。A带正电q,B不带电且用长为L的细绳竖直悬挂在O点。整个空间存在竖直向上的匀强电场，场强大小为E=
A球在M点沿竖直向下射入磁场B，到达N点时速度水平，在N点与B球碰后交换速度，碰后B球刚好能以L为半径，在竖直平面内运动到圆周最高点，A球则水平匀速从Q点射出。(重力加速度为g)不计一切摩擦。已知AB与水平面夹角为45°，BC与水平面夹角为θ，求：
(1)B球被碰后的速度大小。
(2)A球射入点M到N的距离。
(3)A球从Q点水平射出时距N点的距离及θ角。
【解析】(1)A球、B球两球碰后带电量各为
B球从N点到圆周运动的最高点过程中，由动能定理有
在圆周运动的最高点由牛顿第二定律有
mg-E·
联立①②，解得vB=
(2)A球从M到N做圆周运动，由牛顿第二定律有
qvAB=m
又vA=vB=
又由几何关系有sMN=
r
sMN=
(3)（略）
练习册系列答案
开心蛙口算题卡系列答案
相关题目
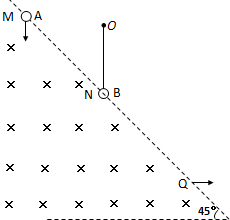如图，虚线的左下方存在匀强磁场B．A，B是完全相同的两个质量均为m的小金属球（可看做质点）．A带正电q，B不带电用细绳竖直悬挂在O点．整个空间存在竖直向上的匀强电场，场强大小为E=mg/q．A球在M点沿竖直向下射入磁场B．在N点与B球发生水平方向完全弹性碰撞，碰后B球刚好能以L为半径，在竖直平面内运动到圆周最高点，A球则水平匀速从Q点射出．（重力加速度为g）不计一切摩擦．
，A球在M点沿竖直向下射入磁场B，到达N点时速度水平，在N点与B球碰后交换速度，碰后B球刚好能以L为半径，在竖直平面内运动到圆周最高点，A球则水平匀速从Q点射出。(重力加速度为g)不计一切摩擦。已知AB与水平面夹角为45°，BC与水平面夹角为θ=30°。
