Question

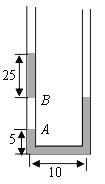
【题目】如图所示，两正对且固定不动的导热气缸，与水平成30°角，底部由体积忽略不计的细管连通、活塞a、b用不可形变的轻直杆相连，不计活塞的厚度以及活塞与气缸的摩擦，a、b两活塞的横截面积分别为S1=10cm2，S2=20cm2，两活塞的总质量为m=12kg，两气缸高度均为H=10cm。气缸内封闭一定质量的理想气体，系统平衡时活塞a、b到气缸底的距离均为L=5cm(图中未标出)，已知大气压强为P=105Pa.环境温度为T0=300K，重力加速度g取10m/s2。求：

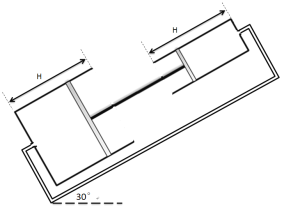
(1)若缓慢降低环境温度，使活塞缓慢移到气缸的一侧底部，求此时环境的温度；

(2)若保持环境温度不变，用沿轻杆向上的力缓慢推活塞，活塞a由开始位置运动到气缸底部，求此过程中推力的最大值。

Answer 1

【答案】(1)200K(2)40N

【解析】

(1)将两活塞作为整体受力分析，求得气缸内气体的压强；缓慢降低环境温度，使活塞缓慢移动时，气体压强不变，体积减小，活塞向下移动；由盖·吕萨克定律可得活塞缓慢移到气缸的一侧底部时环境的温度。

(2) 沿轻杆向上的力缓慢推活塞，活塞a由开始位置运动到气缸底部时，推力最大。求得末状态(活塞a由开始位置运动到气缸底部时)气体的总体积；据玻意耳定律求得末状态气体的压强；将两活塞作为整体受力分析，求得推力的最大值。

(1)设初始气体压强为，将两活塞作为整体受力分析，由平衡条件可得：，代入数据解得：

活塞缓慢移动过程中，缸内气体压强不变，温度降低，体积减小，活塞向下移动；由盖·吕萨克定律可得：，解得：活塞缓慢移到气缸的一侧底部时环境的温度

(2) 沿轻杆向上的力缓慢推活塞，气体体积变化，又气体温度不变，则气体压强变化，当活塞到达汽缸顶部时，向上的推力最大，此时气体的体积为，设此时的压强为，由玻意耳定律得：

代入数据解得：

将两活塞作为整体受力分析，由平衡条件可得：

代入数据解得：