题目内容
6.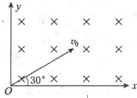 如图所示,在直角坐标系的第一象限内有垂直于纸面向里的匀强磁场(磁场区域足够大),磁感应强度的大小B=0.2T,一带电粒子以初速度v0=1×106m/s、沿与x轴正方向成30°角的方向从原点垂直磁场射入,已知粒子的比荷$\frac{q}{m}$=1×108C/kg,求:
如图所示,在直角坐标系的第一象限内有垂直于纸面向里的匀强磁场(磁场区域足够大),磁感应强度的大小B=0.2T,一带电粒子以初速度v0=1×106m/s、沿与x轴正方向成30°角的方向从原点垂直磁场射入,已知粒子的比荷$\frac{q}{m}$=1×108C/kg,求:(1)粒子在磁场中的运动半径r;
(2)粒子在磁场中的时间t.
分析 (1)粒子在磁场中都做匀速圆周运动,由洛伦兹力充当向心力,由牛顿第二定律求出轨迹半径;
(2)作出粒子的运动轨迹,确定出轨迹所对应的圆心角,根据粒子做圆周运动的周期公式与粒子转过的圆心角可以求出粒子在磁场中运动的时间.
解答 解:(1)粒子在磁场中做圆周运动,洛伦兹力提供向心力,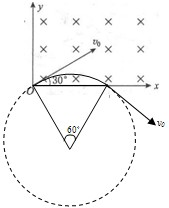
由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{r}$,解得:r=$\frac{m{v}_{0}}{qB}$=$\frac{1×1{0}^{6}}{1×1{0}^{8}×0.2}$=0.05m=5cm;
(2)粒子做圆周运动的周期:T=$\frac{2πm}{qB}$=$\frac{2π}{1×1{0}^{8}×0.2}$=π×10-7s,
粒子运动轨迹如图所示,由几何知识可知,粒子转过的圆心角:θ=60°,
粒子在磁场中的运动时间:t=$\frac{θ}{360°}$T=$\frac{60°}{360°}$×π×10-7=$\frac{π}{6}$×10-7s;
答:(1)粒子在磁场中的运动半径r为5cm;
(2)粒子在磁场中的时间t为$\frac{π}{6}$×10-7s.
点评 本题考查了牛顿第二定律和向心力知识的运用,要注重运用几何知识辅助分析,画出轨迹是基本能力,要加强训练提高能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
16.一个质点正在做匀加速直线运动,用固定的照相机对该质点进行闪光照相,相邻两次闪光的时间间隔为1s.分析照片发现,质点在第1次、第2次闪光的时间间隔内移动了0.2m;在第3次、第4次闪光的时间间隔内移动了0.8m.由上述条件可知( )
| A. | 质点运动的加速度是0.6m/s2 | B. | 质点运动的加速度是0.3m/s2 | ||
| C. | 第1次闪光时质点的速度是0.1m/s | D. | 第2次闪光时质点的速度是0.35m/s |
14. 有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上随地球表面一起转动,b处于地面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星,各卫星排列位置如图所示,则有( )
有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上随地球表面一起转动,b处于地面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星,各卫星排列位置如图所示,则有( )
 有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上随地球表面一起转动,b处于地面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星,各卫星排列位置如图所示,则有( )
有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上随地球表面一起转动,b处于地面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星,各卫星排列位置如图所示,则有( )| A. | a的向心加速度小于重力加速度g | B. | b在相同时间内转过的弧长最长 | ||
| C. | c在4h内转过的圆心角是$\frac{π}{6}$ | D. | d的运动周期有可能是26 小时 |
1.关于速度和加速度关系的下述说法中正确的是( )
| A. | 速度变化得越快,加速度就越大 | |
| B. | 加速度不变,速度不断地变化 | |
| C. | 速度的数值增大,则加速度的数值必增大 | |
| D. | 加速度的数值减小,则速度的数值必减小 |
18.打出的点迹不够清晰的原因可能是?( )
| A. | 电源电压偏低 | B. | 永磁体磁性不足 | C. | 振针位置过高 | D. | 复写纸陈旧 |
15.某个物体带电量不可能是( )
| A. | 2×10-19 C | B. | 3.2×10-19 C | C. | 4.8×10-19 C | D. | 6×10-6 C |
16.关于电源,下列说法正确的是( )
| A. | 当电池用旧之后,电动势减小,内阻也减小 | |
| B. | 对同一种电池,体积越大电池容量越小 | |
| C. | 电源的电动势与外电路无关 | |
| D. | 电池的电容量表示电池放电时能输出的电能 |
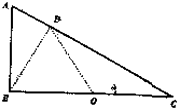 如图所示,直角三角形的斜边倾角为30°,底边BC长为2L,处在水平位置,斜边AC是光滑绝缘的,在底边中点O处放置一正电荷Q,一个质量为m,电量为q的带负电的质点从斜面顶端A沿斜边滑下,滑到斜边上的垂足D时加速度为a,求即将滑到斜边上的C点时的加速度.(结果只能保留g、a)
如图所示,直角三角形的斜边倾角为30°,底边BC长为2L,处在水平位置,斜边AC是光滑绝缘的,在底边中点O处放置一正电荷Q,一个质量为m,电量为q的带负电的质点从斜面顶端A沿斜边滑下,滑到斜边上的垂足D时加速度为a,求即将滑到斜边上的C点时的加速度.(结果只能保留g、a)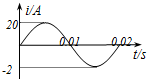 如图所示为正弦交流电图线,由图可知该交变电流的最大值是20A,有效值是10$\sqrt{2}$A,频率为50Hz,电流瞬时值表达式是i=20sin100πt.
如图所示为正弦交流电图线,由图可知该交变电流的最大值是20A,有效值是10$\sqrt{2}$A,频率为50Hz,电流瞬时值表达式是i=20sin100πt.