题目内容
17．
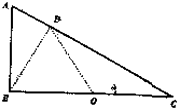如图所示，直角三角形的斜边倾角为30°，底边BC长为2L，处在水平位置，斜边AC是光滑绝缘的，在底边中点O处放置一正电荷Q，一个质量为m，电量为q的带负电的质点从斜面顶端A沿斜边滑下，滑到斜边上的垂足D时加速度为a，求即将滑到斜边上的C点时的加速度．（结果只能保留g、a）
分析 根据几何知识分析得到B、C、D三点在以O为圆心的同一圆周上，三点的场强大小相等．分析质点q在C点的受力情况，根据牛顿第二定律和库仑定律求出质点滑到斜边底端C点时加速度
解答 解：由题，BD⊥AC，O点是BC的中点，根据几何知识得到B、C、D三点在以O为圆心的同一圆周上，质点在D点受三个力的作用；电场F，方向由O指向D点；重力mg，方向竖直向下；支持力N，方向垂直于斜面向上．由牛顿第二定律，有：
mgsin30°-Fcos30°=ma…①
质点在C受三个力的作用；电场F，方向由O指向C点；重力mg，方向竖直向下；支持力N，方向垂直于斜面向上．由牛顿第二定律，有：
mgsin30°+Fcos30°=maC…②
由①②得：aC=g-a
答：即将滑到斜边上的C点时的加速度g-a
点评 本题难点在于分析D与C两点电场强度相等，由牛顿第二定律求加速度都常规思路
练习册系列答案
相关题目
7．有一毫安表，它的内阻是100Ω，量程为2mA，现要将它改装成量程为10A的电流表，则毫安表应（ ）
| A． | 并联一个0.02Ω的电阻 | B． | 并联一个0.2Ω的电阻 | ||
| C． | 串联一个50Ω的电阻 | D． | 串联一个4900Ω的电阻 |
8．
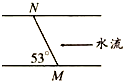如图所示，在一段河岸平直的河中，一船夫划小船由M点出发沿直线到达对岸N点，直线MN与河岸成53°角．已知河宽为48m．河中水流的速度大小为v=5.0m/s，船夫划船在静水中的速度大小为5.0m/s，则小船过河的时间为（sin53°=0.8）（ ）
如图所示，在一段河岸平直的河中，一船夫划小船由M点出发沿直线到达对岸N点，直线MN与河岸成53°角．已知河宽为48m．河中水流的速度大小为v=5.0m/s，船夫划船在静水中的速度大小为5.0m/s，则小船过河的时间为（sin53°=0.8）（ ）| A． | 4.8s | B． | l0s | C． | 14.4s | D． | 20s |
5．一定质量的理想气体经过一系列变化过程，下列说法中正确的是 （ ）
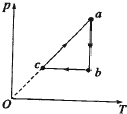
| A． | b→c过程中，气体压强不变，体积增大 | |
| B． | a→b过程中，气体体积增大，压强减小 | |
| C． | c→a过程中，气体压强增大，体积变小 | |
| D． | c→a过程中，气体内能增大，体积变小 | |
| E． | c→a过程中，气体从外界吸热，内能增加 |
2．我国发射是“亚洲一号”地球同步通讯卫星的质量为1.2t，在某一确定的轨道上运行，下列说法中正确的是 （ ）
| A． | 它可以定位在北京正上方太空 | |
| B． | 它的轨道平面一定与赤道平面重合 | |
| C． | 若要发射一颗质量为2.4t的地球同步卫星，则该卫星的轨道半径将比“亚洲一号”卫星的轨道半径小 | |
| D． | 若发射质量为2.4t的地球同步卫星，则该卫星的轨道半径将比“亚洲一号”卫星的轨道半径大 |
9．
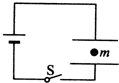图中两板间距为d的平行板电容器与一电源连接，电健s闭合，电容器两板间有一质量为m，电量为q的微粒静止不动，下列说法中正确的是（ ）
图中两板间距为d的平行板电容器与一电源连接，电健s闭合，电容器两板间有一质量为m，电量为q的微粒静止不动，下列说法中正确的是（ ）| A． | 微粒带正电 | |
| B． | 增大电容器两极板间距离，微粒向下运动 | |
| C． | 电源两端电压为mgd/q | |
| D． | 断开电键s，微粒向下运动 |
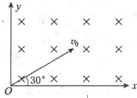如图所示，在直角坐标系的第一象限内有垂直于纸面向里的匀强磁场（磁场区域足够大），磁感应强度的大小B=0.2T，一带电粒子以初速度v0=1×106m/s、沿与x轴正方向成30°角的方向从原点垂直磁场射入，已知粒子的比荷$\frac{q}{m}$=1×108C/kg，求：
