题目内容
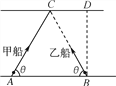
【题目】如图所示,甲、乙两船在同一河岸边A、B两处,两船船头方向与河岸均成θ角,且恰好对准对岸边C点。若两船同时开始渡河,经过一段时间t,同时到达对岸,乙船恰好到达正对岸的D点。若河宽d、河水流速均恒定,两船在静水中的划行速率恒定,且不影响各自的航行。下列说法中正确的是 ( )
A. 两船在静水中的划行速率不同
B. 甲船渡河的路程有可能比乙船渡河的路程小
C. 两船同时到达D点
D. 河水流速为![]()
【答案】C
【解析】A. 由题意可知,两船渡河的时间相等,两船沿垂直河岸方向的分速度υ1相等,由υ1=υsinθ知两船在静水中的划行速率υ相等,选项A错误;
B. 乙船沿BD到达D点,可见河水流速υ水方向沿AB方向,可见甲船不可能到达到正对岸,甲船渡河的路程较大,选项B错误;
C. 由于甲船沿AB方向的位移大小x=(υcosθ+υ水)t=2dtanθ=AB,可见两船同时到达D点,选项C正确;
D. 根据速度的合成与分解,υ水=υcosθ,而υsinθ=d/t,得![]() ,选项D错误;
,选项D错误;
故选:C.
小船过河的速度为船在静水中的速度垂直河岸方向的分速度,故要求过河时间需要将船速分解为沿河岸的速度和垂直河岸的速度;要求两船相遇的地点,需要求出两船之间的相对速度,即它们各自沿河岸的速度的和.

练习册系列答案
相关题目