题目内容
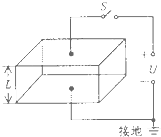 为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上、下底面都是而积为A的金属板,间距为L,金属板连接到电压为U的高压电源正负极,如图所示,现把定量均匀分布的烟尘颗粒密闭在容器内,单位体积内烟尘颗粒数为n,假设这些颗粒都处于静止状态,每个颗粒质量为m,带有电量为q的正电荷,碰到下极板时会被极板吸附,不考虑颗粒之间的相瓦作用、空气阻力以及颗粒所受重力,求合上电键后:
为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上、下底面都是而积为A的金属板,间距为L,金属板连接到电压为U的高压电源正负极,如图所示,现把定量均匀分布的烟尘颗粒密闭在容器内,单位体积内烟尘颗粒数为n,假设这些颗粒都处于静止状态,每个颗粒质量为m,带有电量为q的正电荷,碰到下极板时会被极板吸附,不考虑颗粒之间的相瓦作用、空气阻力以及颗粒所受重力,求合上电键后:(1)经过多长时间烟尘颗粒可以被全部吸附?
(2)将烟尘完全除掉,电场对烟尘共做多少功?
(3)经过多长时间容器中烟尘颗粒的总动能达到最大?
分析:在本题中带电颗粒做初速度为零的匀加速运动直到到达负极板为止,当离负极板最远的粒子到达负极板时,所有颗粒全部被吸收;由于颗粒均匀分布在密闭容器内,可以等效为所有颗粒从两极板中间被加速到负极板,从而求出电场对颗粒做的总功;写出动能表达式,利用数学知识和运动学公式可以求出经过多长时间颗粒的总动能最大.
解答:解:(1)当最靠近上板的尘粒运动到下板时,全部烟尘就被吸附,
设需时间t
烟尘颗粒受到的电场力
F=qE=
从盒子最上端运动到盒底的尘粒运动时间设为t
则L=
at2
t=
(2)设容器容积为V,电源接通前尘粒总数为N,
则N=nV=nLA
电场对烟尘做的总功W=
NqU
=
nALqU
(3)设原先位于盒顶的尘粒下落距离x时,部分尘粒已被下极板吸附,容器内未被吸附的尘粒数为
nA(L-x)
它们的总动能设为EK,
则 EK=nA(L-x).
mv2=
式中的因式(L-x)x=-(x2-Lx+
)+
=
-(x-
)2,
当x=
时该因式有最大值
故 当x=
时,EK达最大
设此时刻为t1则x=
at12
求得t1=
答:(1)经过
时间烟尘颗粒可以被全部吸附;
(2)将烟尘完全除掉,电场对烟尘共做功为
nALqU;
(3)经过时间
,容器中烟尘颗粒的总动能达到最大.
设需时间t
烟尘颗粒受到的电场力
F=qE=
| qU |
| L |
从盒子最上端运动到盒底的尘粒运动时间设为t
则L=
| 1 |
| 2 |
t=
|
(2)设容器容积为V,电源接通前尘粒总数为N,
则N=nV=nLA
电场对烟尘做的总功W=
| 1 |
| 2 |
=
| 1 |
| 2 |
(3)设原先位于盒顶的尘粒下落距离x时,部分尘粒已被下极板吸附,容器内未被吸附的尘粒数为
nA(L-x)
它们的总动能设为EK,
则 EK=nA(L-x).
| 1 |
| 2 |
| n(L-X)?qxU |
| L |
式中的因式(L-x)x=-(x2-Lx+
| L2 |
| 4 |
| L2 |
| 4 |
| L2 |
| 4 |
| L |
| 2 |
当x=
| L |
| 2 |
故 当x=
| L |
| 2 |
设此时刻为t1则x=
| 1 |
| 2 |
求得t1=
|
答:(1)经过
|
(2)将烟尘完全除掉,电场对烟尘共做功为
| 1 |
| 2 |
(3)经过时间
|
点评:本题属于较难题目,要正确建立物理模型,依据相关物理规律求解.

练习册系列答案
相关题目
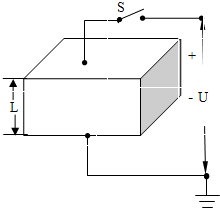 为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是金属板,当连接到高压电源正负两极时,能在两金属板间产生一个电场,如图所示.现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒1013个,每个颗粒带正电荷,假设这些颗粒都处于静止状态,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力,则合上开关后( )
为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是金属板,当连接到高压电源正负两极时,能在两金属板间产生一个电场,如图所示.现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒1013个,每个颗粒带正电荷,假设这些颗粒都处于静止状态,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力,则合上开关后( ) 为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是面积A=0.04m2的金属板,间距L=0.05m,当连接到U=2500V的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示,现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒1013个,假设这些颗粒都处于静止状态,每个颗粒带电量为q=+1.0×10-17C,质量为m=2.0×10-15kg,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力.求合上电键后:
为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是面积A=0.04m2的金属板,间距L=0.05m,当连接到U=2500V的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示,现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒1013个,假设这些颗粒都处于静止状态,每个颗粒带电量为q=+1.0×10-17C,质量为m=2.0×10-15kg,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力.求合上电键后: