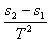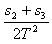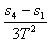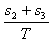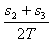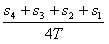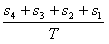题目内容
在研究小车速度随时间变化规律的实验中,得到一条记录小车运动情况的点迹清晰的纸带,如图3-2-6所示,图中A、B、C、D、E为相邻计数点,相邻计数点的时间间隔T=0.1 s.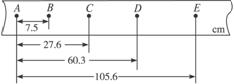
图3-2-6
(1)根据纸带上的数据,计算各点速度,填入下表中.
位置编号 | A | B | C | D | E |
时间t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 |
瞬时速度v/(m·s-1) |
|
|
|
|
|
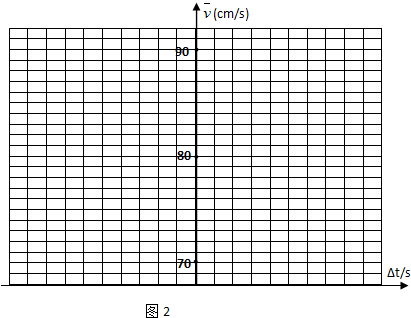
(2)在图3-2-7中作出小车的v-t图线.

图3-2-7
解析:(1)由纸带标明的数据可以计算任意相邻两位置之间的位移,然后求纸带上各点的速度和加速度.由纸带的标注可以求出
xAB=7.5 cm
xBC=xAC-xAB=(27.6-7.5) cm=20.1 cm
xCD=xAD-xAC=(60.3-27.6) cm=32.7 cm
xDE=xAE-xAD=(105.6-60.3) cm=45.3 cm
相邻的相等时间位移差
Δx1=xBC-xAB=(20.1-7.5) cm=12.6 cm
Δx2=xCD-xBC=(32.7-20.1) cm=12.6 cm
Δx3=xDE-xCD=(45.3-32.7) cm=12.6 cm
即Δx1=Δx2=Δx3
所以纸带做匀变速直线运动,其加速度
a=![]() =
=![]() m/s2=12.6 m/s2
m/s2=12.6 m/s2
匀变速直线运动物体在一段时间内的平均速度等于该时间中间时刻的瞬时速
度,所以
vB=![]() =
=![]() m/s=1.38 m/s
m/s=1.38 m/s
vC=![]() =
=![]() m/s=2.64 m/s
m/s=2.64 m/s
vD=![]() =
=![]() m/s=3.90 m/s
m/s=3.90 m/s
vA=vB-aT=1.38 m/s-12.6×0.1 m/s=0.12 m/s
vE=vD+aT=3.90 m/s+12.6×0.1 m/s=5.16 m/s
分别填入表中对应位置即可.
(2)在图上取合适的单位严格描点,可看出这些点大致分布在一条直线上,用直线连接这些点,使尽可能多的点分布在该直线上,不能位于直线上的点要尽量对称分布于直线两侧,便得到小车的v-t图象,由图象斜率也可得到小车的加速度为12.6 m/s2.

 阅读快车系列答案
阅读快车系列答案
 A.选修3-3
A.选修3-3


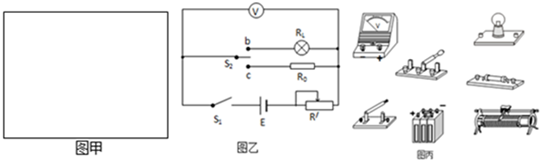
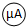 :量程0~200μA、内阻500Ω
:量程0~200μA、内阻500Ω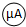 改装成一个量程略大于2.5V的伏特表,将改装表的电路图画在图甲的方框内,此伏特表
改装成一个量程略大于2.5V的伏特表,将改装表的电路图画在图甲的方框内,此伏特表 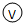 的量程是
的量程是 和选用的器材设计如图乙所示的电路,来测量通过小灯泡的电流强度,请在图丙的实物图上连线
和选用的器材设计如图乙所示的电路,来测量通过小灯泡的电流强度,请在图丙的实物图上连线 的示数为1.5V,则通过小灯泡的电流强度为
的示数为1.5V,则通过小灯泡的电流强度为