题目内容
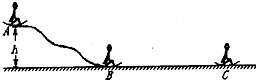 如图所示,某人乘雪橇从雪坡A点滑至B点,接着沿水平地面滑至C点停止.人与雪橇的总质量为70kg,A点距地面的高度为20m,人与雪橇在BC段所受阻力恒定.图表中记录了人与雪橇运动过程中的有关数据.求:(取g=10m/s2)
如图所示,某人乘雪橇从雪坡A点滑至B点,接着沿水平地面滑至C点停止.人与雪橇的总质量为70kg,A点距地面的高度为20m,人与雪橇在BC段所受阻力恒定.图表中记录了人与雪橇运动过程中的有关数据.求:(取g=10m/s2)| 位置 | A | B | C |
| 速度(m/s) | 2.0 | 12.0 | 0 |
| 时刻(s) | 0 | 4.0 | 10.0 |
(2)人与雪橇在BC颇受阻力的大小;
(3)BC的距离.
分析:(1)选人与雪橇作为研究对象,由于存在阻力做功,导致系统的机械能不守恒,因而分别求出两点的机械能,则两者之差即为损失的机械能;
(2)人与雪橇在BC段的初、末速度可以根据a=
,求出加速度,再由牛顿第二定律可求出阻力.
(3)根据动能定理可求出BC段距离.
(2)人与雪橇在BC段的初、末速度可以根据a=
| v-v0 |
| t |
(3)根据动能定理可求出BC段距离.
解答:解:(1)从A到B的过程中,人与雪橇损失的机械能为:
△E=mgh+
m
-
m
①
代入数据解得:△E=9100J
(2)人与雪橇在BC段做减速运动的加速度:a=
②
根据牛顿第二定律:Ff=ma ③
由②③得:Ff=140N
(3)由动能定理得:-Ffx=0-
m
代入数据解得:x=36m
答:(1)人与雪橇从A到B的过程中,损失的机械能为9100J;
(2)人与雪橇在BC颇受阻力的大小是140N;
(3)BC的距离为36m.
△E=mgh+
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
代入数据解得:△E=9100J
(2)人与雪橇在BC段做减速运动的加速度:a=
| vC-vB |
| △t |
根据牛顿第二定律:Ff=ma ③
由②③得:Ff=140N
(3)由动能定理得:-Ffx=0-
| 1 |
| 2 |
| v | 2 B |
代入数据解得:x=36m
答:(1)人与雪橇从A到B的过程中,损失的机械能为9100J;
(2)人与雪橇在BC颇受阻力的大小是140N;
(3)BC的距离为36m.
点评:考查机械能守恒定律的条件、动能定理、牛顿第二定律、运动学公式,注意动能定理中功的正负值,本题是简单的力学综合题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 (2005?上海)如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:
(2005?上海)如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题: (2008?嘉定区二模)如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止(人与雪橇在B点无能量损失).人与雪橇的总质量为70kg.设雪橇与AB、BC接触面间的动摩擦因数处处相同,忽略空气阻力,表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:
(2008?嘉定区二模)如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止(人与雪橇在B点无能量损失).人与雪橇的总质量为70kg.设雪橇与AB、BC接触面间的动摩擦因数处处相同,忽略空气阻力,表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题: 如图所示,某人乘雪橇从雪坡A点滑至B点,接着沿水平路面滑至C点停止.若人与雪橇的总质量为70kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:(取g=10m/s2)
如图所示,某人乘雪橇从雪坡A点滑至B点,接着沿水平路面滑至C点停止.若人与雪橇的总质量为70kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:(取g=10m/s2)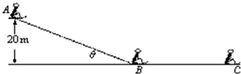 如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止(人与雪橇在B点无能量损失).人与雪橇的总质量为80kg,A点距地面高度20m.设雪橇与AB、BC接触面间的动摩擦因数处处相同,忽略空气阻力,表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:(g=10m/s2)
如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止(人与雪橇在B点无能量损失).人与雪橇的总质量为80kg,A点距地面高度20m.设雪橇与AB、BC接触面间的动摩擦因数处处相同,忽略空气阻力,表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:(g=10m/s2)