题目内容
（2008?嘉定区二模）如图所示，某人乘雪橇从雪坡经A点滑至B点，接着沿水平路面滑至C点停止（人与雪橇在B点无能量损失）．人与雪橇的总质量为70kg．设雪橇与AB、BC接触面间的动摩擦因数处处相同，忽略空气阻力，表中记录了沿坡滑下过程中的有关数据，请根据图表中的数据解决下列问题：| 位置 | A | B | C |
| 速度（m/s） | 2.0 | 15.2 | 0 |
| 时刻（s） | 0 | 3 | 10.6 |
（2）求斜面的倾角θ．
分析：（1）在BC段通过运动学公式把加速度求出，然后利用牛顿第二定律求出摩擦因数
（2）在AB段先通过运动学公式求出加速度，然后利用牛顿第二定律求出倾角
（2）在AB段先通过运动学公式求出加速度，然后利用牛顿第二定律求出倾角
解答：解：（1）人与雪橇在BC段的加速度为：
a2=
=
m/s=-2m/s2
根据牛顿第二定律有：f=μgm=ma2
得：μ=0.2
（2）设人与雪橇在AB段的加速度a1，由vB=vA+a1t1得：
a1=
=
=4.4m/s2
由牛顿第二定律可知：
mgsinθ-μmgcosθ=ma1
得：a1=gsinθ-μgcosθ
代入数据求得：θ=37°
答：（1）动摩擦因数μ为0.2；
（2）斜面的倾角θ为37°．
a2=
| vC-vB |
| t |
| 0-15.2 |
| 10.6-3 |
根据牛顿第二定律有：f=μgm=ma2
得：μ=0.2
（2）设人与雪橇在AB段的加速度a1，由vB=vA+a1t1得：
a1=
| vB-vA |
| t1 |
| 15.2-2.0 |
| 3.0-0 |
由牛顿第二定律可知：
mgsinθ-μmgcosθ=ma1
得：a1=gsinθ-μgcosθ
代入数据求得：θ=37°
答：（1）动摩擦因数μ为0.2；
（2）斜面的倾角θ为37°．
点评：根据人的运动的过程，应用牛顿第二定律和运动学的公式可以直接求解，题目比较简单．
练习册系列答案
相关题目
（2008?嘉定区二模）一列沿x轴传播的简谐横波某时刻的波形图象如图甲所示．若从此时刻开始计时，则图乙表示a、b、c、d中哪个质点的振动图象（ ）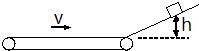
（2008?嘉定区二模）如图所示，小物块从光滑斜面距底边h=0.8m高处由静止下滑，经一与斜面相切的小圆弧滑上足够长的正在匀速运转的水平传送带，传送带的速度为v，方向如图，经过一定时间后，物块从传送带上返回又冲上斜面．当v=3m/s时物块能冲上斜面的高度h1=
（2008?嘉定区二模）如图所示，边长为L的正方形区域abcd内存在着匀强磁场．